Occam factors and model-independent Bayesian learning of continuous distributions
Paper and Code
Feb 05, 2002

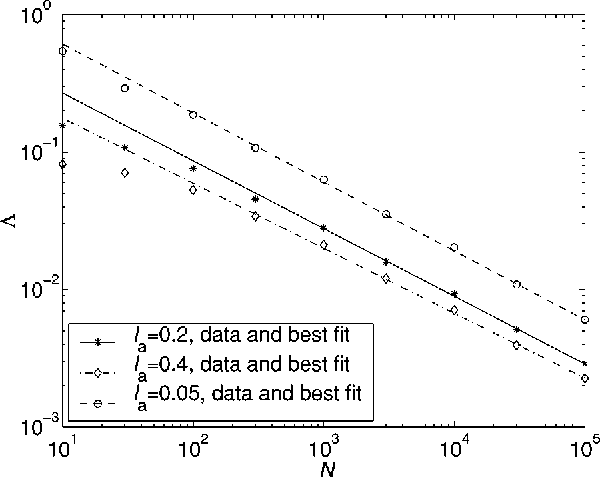
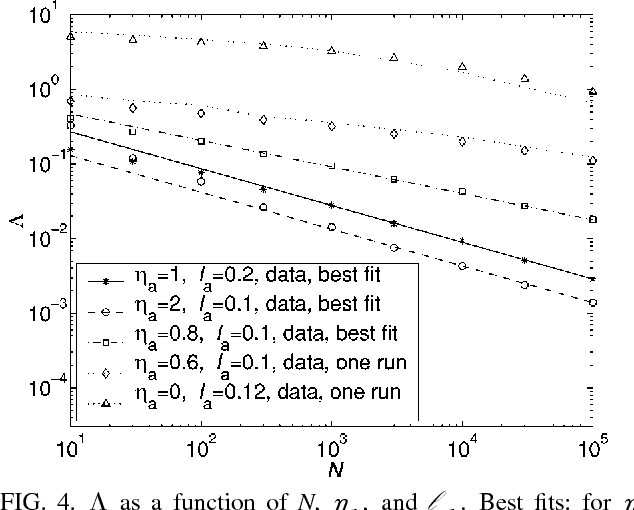
Learning of a smooth but nonparametric probability density can be regularized using methods of Quantum Field Theory. We implement a field theoretic prior numerically, test its efficacy, and show that the data and the phase space factors arising from the integration over the model space determine the free parameter of the theory ("smoothness scale") self-consistently. This persists even for distributions that are atypical in the prior and is a step towards a model-independent theory for learning continuous distributions. Finally, we point out that a wrong parameterization of a model family may sometimes be advantageous for small data sets.
* Phys. Rev. E, 65 (2), 2002 * publication revisions: extended introduction, new references, other
minor corrections; 6 pages, 6 figures, revtex
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge