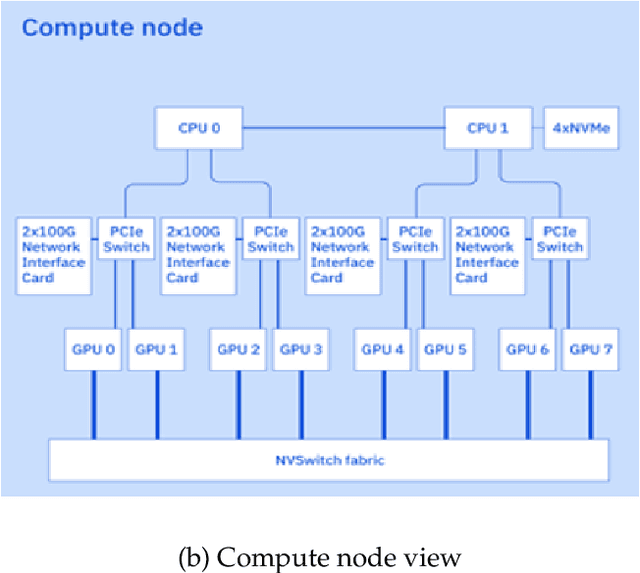
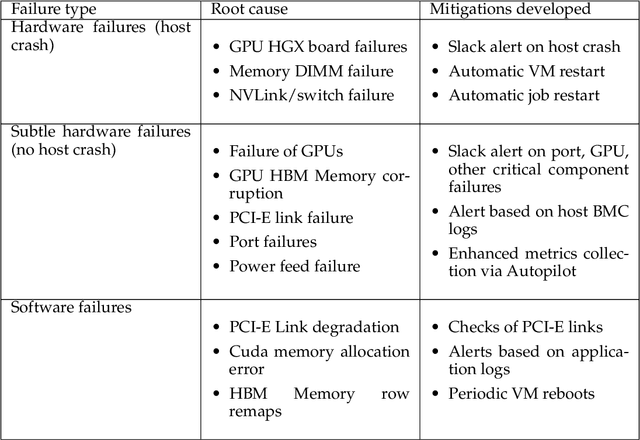
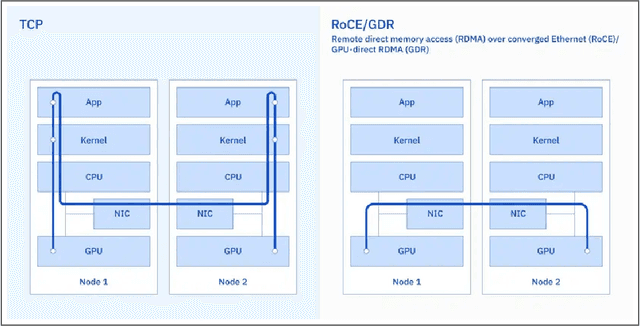
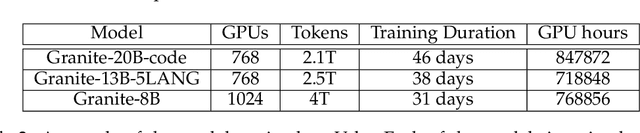
The infrastructure powering IBM's Gen AI model development

AI Infrastructure plays a key role in the speed and cost-competitiveness of developing and deploying advanced AI models. The current demand for powerful AI infrastructure for model training is driven by the emergence of generative AI and foundational models, where on occasion thousands of GPUs must cooperate on a single training job for the model to be trained in a reasonable time. Delivering efficient and high-performing AI training requires an end-to-end solution that combines hardware, software and holistic telemetry to cater for multiple types of AI workloads. In this report, we describe IBM's hybrid cloud infrastructure that powers our generative AI model development. This infrastructure includes (1) Vela: an AI-optimized supercomputing capability directly integrated into the IBM Cloud, delivering scalable, dynamic, multi-tenant and geographically distributed infrastructure for large-scale model training and other AI workflow steps and (2) Blue Vela: a large-scale, purpose-built, on-premises hosting environment that is optimized to support our largest and most ambitious AI model training tasks. Vela provides IBM with the dual benefit of high performance for internal use along with the flexibility to adapt to an evolving commercial landscape. Blue Vela provides us with the benefits of rapid development of our largest and most ambitious models, as well as future-proofing against the evolving model landscape in the industry. Taken together, they provide IBM with the ability to rapidly innovate in the development of both AI models and commercial offerings.

A Comparison of Model-Free and Model Predictive Control for Price Responsive Water Heaters

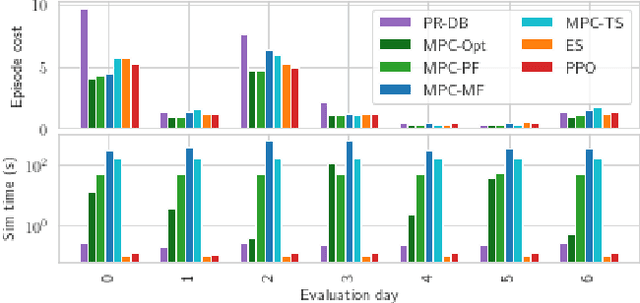
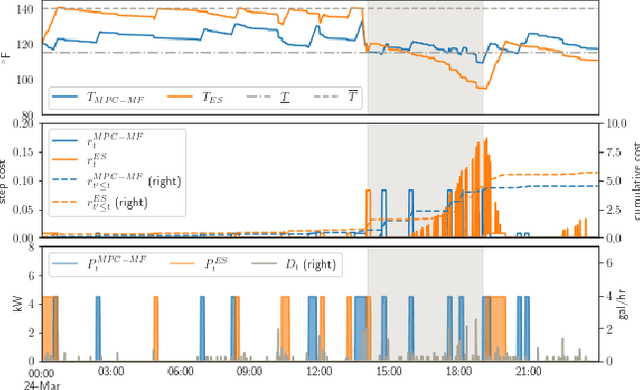
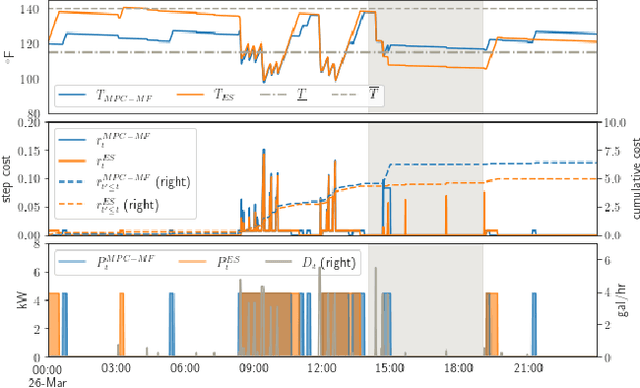
We present a careful comparison of two model-free control algorithms, Evolution Strategies (ES) and Proximal Policy Optimization (PPO), with receding horizon model predictive control (MPC) for operating simulated, price responsive water heaters. Four MPC variants are considered: a one-shot controller with perfect forecasting yielding optimal control; a limited-horizon controller with perfect forecasting; a mean forecasting-based controller; and a two-stage stochastic programming controller using historical scenarios. In all cases, the MPC model for water temperature and electricity price are exact; only water demand is uncertain. For comparison, both ES and PPO learn neural network-based policies by directly interacting with the simulated environment under the same scenarios used by MPC. All methods are then evaluated on a separate one-week continuation of the demand time series. We demonstrate that optimal control for this problem is challenging, requiring more than 8-hour lookahead for MPC with perfect forecasting to attain the minimum cost. Despite this challenge, both ES and PPO learn good general purpose policies that outperform mean forecast and two-stage stochastic MPC controllers in terms of average cost and are more than two orders of magnitude faster at computing actions. We show that ES in particular can leverage parallelism to learn a policy in under 90 seconds using 1150 CPU cores.

K-spin Hamiltonian for quantum-resolvable Markov decision processes

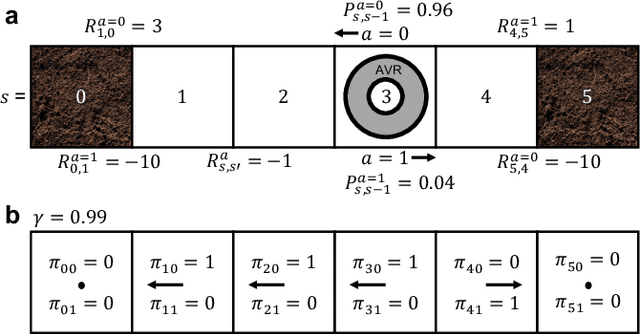
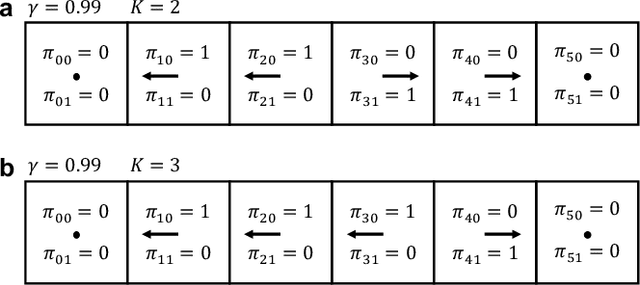
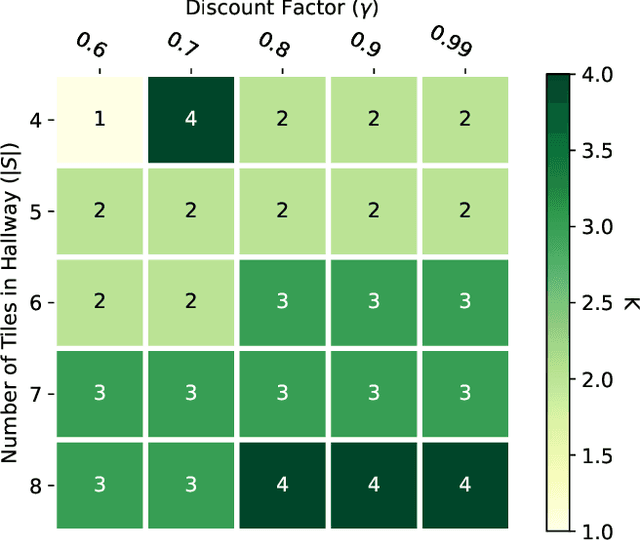
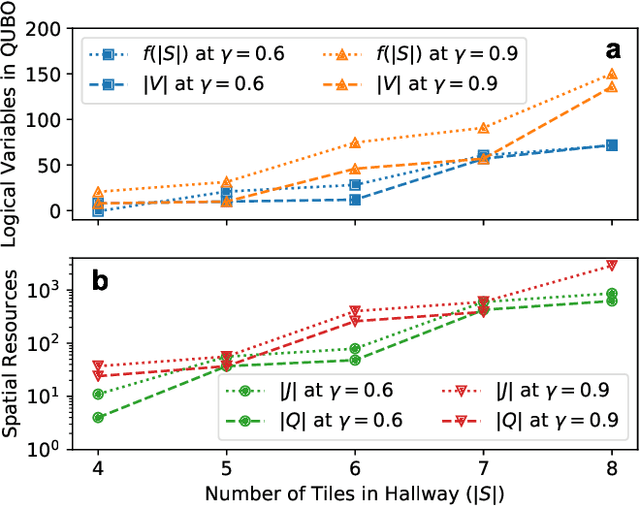
The Markov decision process is the mathematical formalization underlying the modern field of reinforcement learning when transition and reward functions are unknown. We derive a pseudo-Boolean cost function that is equivalent to a K-spin Hamiltonian representation of the discrete, finite, discounted Markov decision process with infinite horizon. This K-spin Hamiltonian furnishes a starting point from which to solve for an optimal policy using heuristic quantum algorithms such as adiabatic quantum annealing and the quantum approximate optimization algorithm on near-term quantum hardware. In proving that the variational minimization of our Hamiltonian is equivalent to the Bellman optimality condition we establish an interesting analogy with classical field theory. Along with proof-of-concept calculations to corroborate our formulation by simulated and quantum annealing against classical Q-Learning, we analyze the scaling of physical resources required to solve our Hamiltonian on quantum hardware.

Keeping greed good: sparse regression under design uncertainty with application to biomass characterization

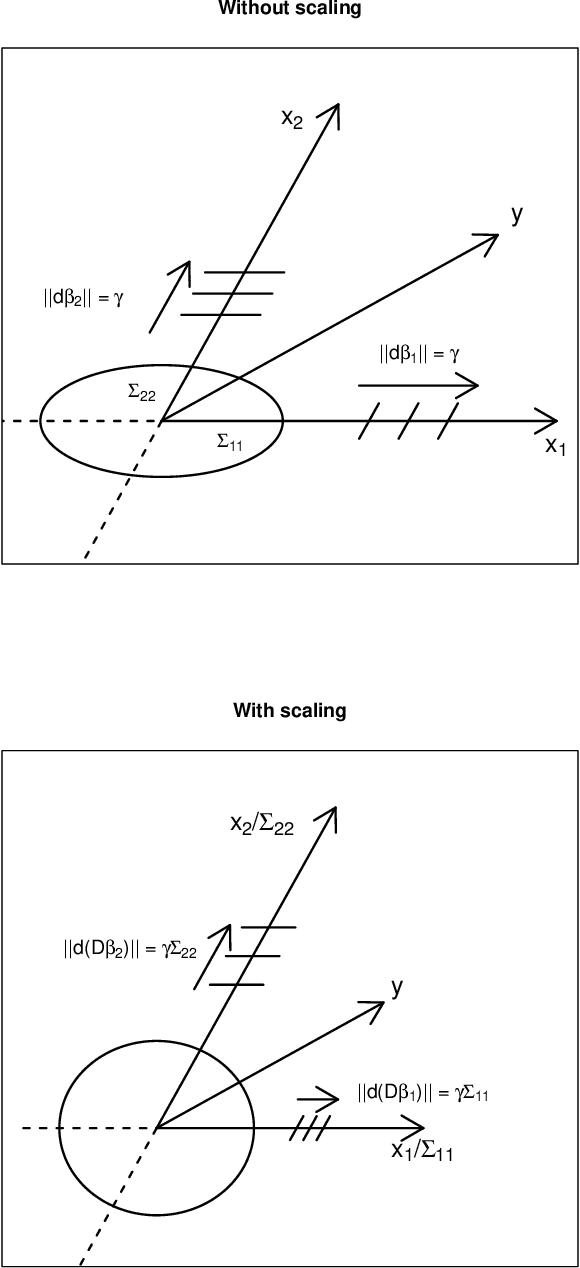
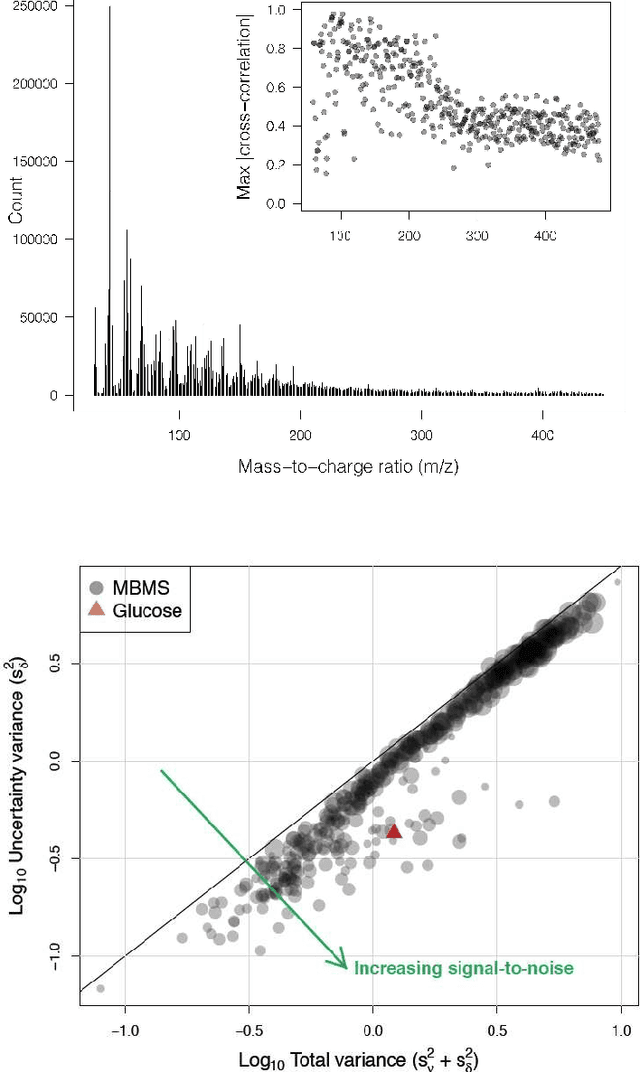
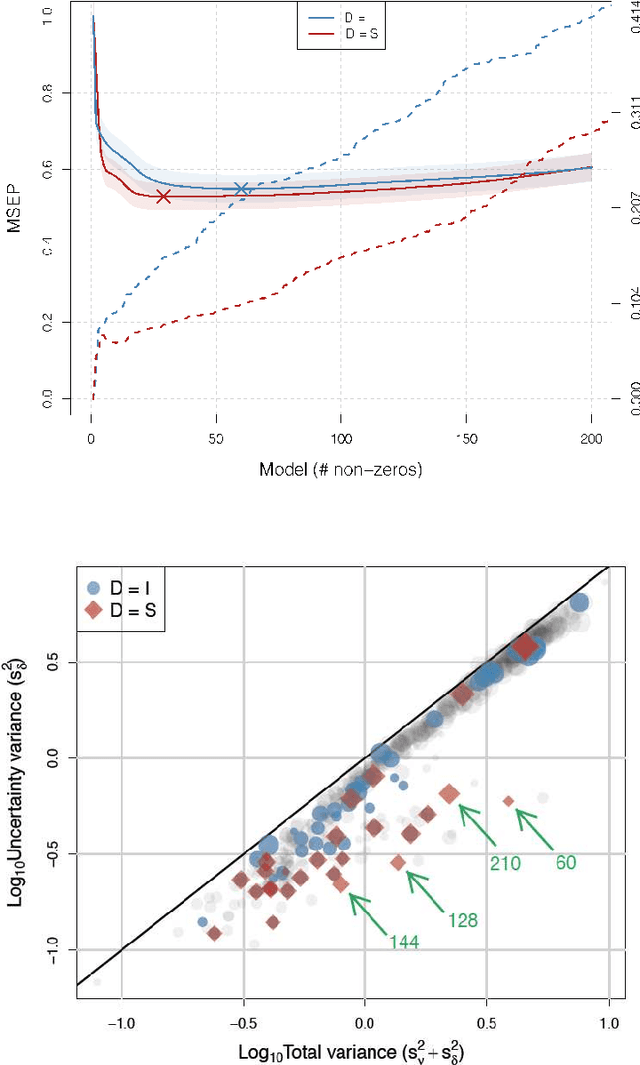
In this paper, we consider the classic measurement error regression scenario in which our independent, or design, variables are observed with several sources of additive noise. We will show that our motivating example's replicated measurements on both the design and dependent variables may be leveraged to enhance a sparse regression algorithm. Specifically, we estimate the variance and use it to scale our design variables. We demonstrate the efficacy of scaling from several points of view and validate it empirically with a biomass characterization data set using two of the most widely used sparse algorithms: least angle regression (LARS) and the Dantzig selector (DS).