Eliot Kapit
K-spin Hamiltonian for quantum-resolvable Markov decision processes
Apr 13, 2020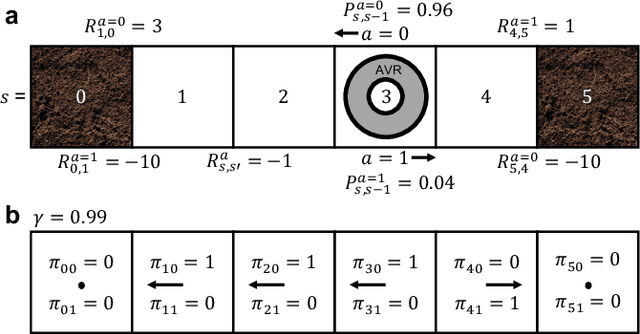
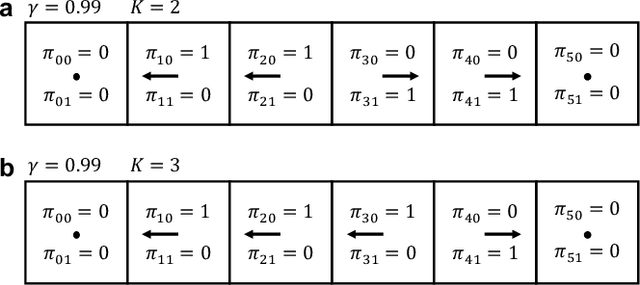
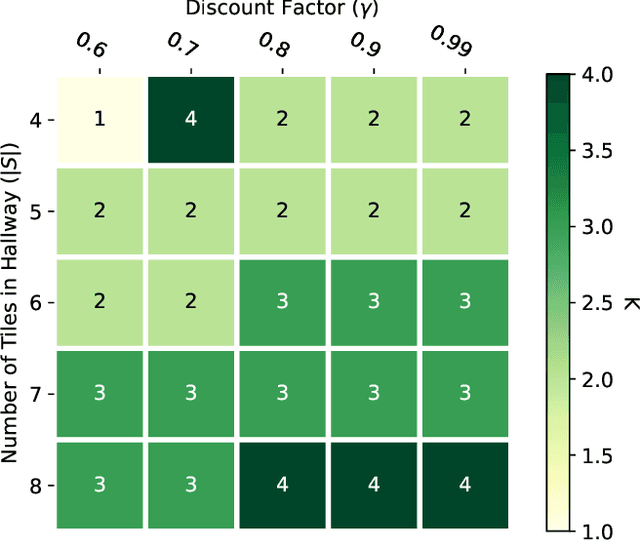
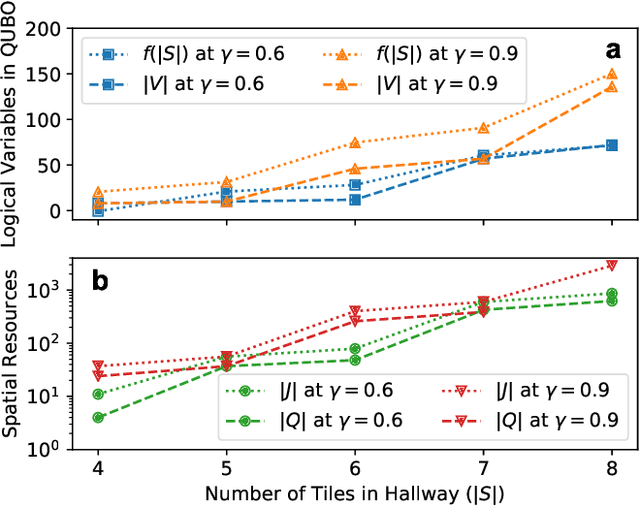
Abstract:The Markov decision process is the mathematical formalization underlying the modern field of reinforcement learning when transition and reward functions are unknown. We derive a pseudo-Boolean cost function that is equivalent to a K-spin Hamiltonian representation of the discrete, finite, discounted Markov decision process with infinite horizon. This K-spin Hamiltonian furnishes a starting point from which to solve for an optimal policy using heuristic quantum algorithms such as adiabatic quantum annealing and the quantum approximate optimization algorithm on near-term quantum hardware. In proving that the variational minimization of our Hamiltonian is equivalent to the Bellman optimality condition we establish an interesting analogy with classical field theory. Along with proof-of-concept calculations to corroborate our formulation by simulated and quantum annealing against classical Q-Learning, we analyze the scaling of physical resources required to solve our Hamiltonian on quantum hardware.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge