A Unified Calibration Framework for Coordinate and Kinematic Parameters in Dual-Arm Robots

Precise collaboration in vision-based dual-arm robot systems requires accurate system calibration. Recent dual-robot calibration methods have achieved strong performance by simultaneously solving multiple coordinate transformations. However, these methods either treat kinematic errors as implicit noise or handle them through separated error modeling, resulting in non-negligible accumulated errors. In this paper, we present a novel framework for unified calibration of the coordinate transformations and kinematic parameters in both robot arms. Our key idea is to unify all the tightly coupled parameters within a single Lie-algebraic formulation. To this end, we construct a consolidated error model grounded in the product-of-exponentials formula, which naturally integrates the coordinate and kinematic parameters in twist forms. Our model introduces no artificial error separation and thus greatly mitigates the error propagation. In addition, we derive a closed-form analytical Jacobian from this model using Lie derivatives. By exploring the Jacobian rank property, we analyze the identifiability of all calibration parameters and show that our joint optimization is well-posed under mild conditions. This enables off-the-shelf iterative solvers to stably optimize these parameters on the manifold space. Besides, to ensure robust convergence of our joint optimization, we develop a certifiably correct algorithm for initializing the unknown coordinates. Relying on semidefinite relaxation, our algorithm can yield a reliable estimate whose near-global optimality can be verified a posteriori. Extensive experiments validate the superior accuracy of our approach over previous baselines under identical visual measurements. Meanwhile, our certifiable initialization consistently outperforms several coordinate-only baselines, proving its reliability as a starting point for joint optimization.

VADTree: Explainable Training-Free Video Anomaly Detection via Hierarchical Granularity-Aware Tree

Video anomaly detection (VAD) focuses on identifying anomalies in videos. Supervised methods demand substantial in-domain training data and fail to deliver clear explanations for anomalies. In contrast, training-free methods leverage the knowledge reserves and language interactivity of large pre-trained models to detect anomalies. However, the current fixed-length temporal window sampling approaches struggle to accurately capture anomalies with varying temporal spans. Therefore, we propose VADTree that utilizes a Hierarchical Granularityaware Tree (HGTree) structure for flexible sampling in VAD. VADTree leverages the knowledge embedded in a pre-trained Generic Event Boundary Detection (GEBD) model to characterize potential anomaly event boundaries. Specifically, VADTree decomposes the video into generic event nodes based on boundary confidence, and performs adaptive coarse-fine hierarchical structuring and redundancy removal to construct the HGTree. Then, the multi-dimensional priors are injected into the visual language models (VLMs) to enhance the node-wise anomaly perception, and anomaly reasoning for generic event nodes is achieved via large language models (LLMs). Finally, an inter-cluster node correlation method is used to integrate the multi-granularity anomaly scores. Extensive experiments on three challenging datasets demonstrate that VADTree achieves state-of-the-art performance in training-free settings while drastically reducing the number of sampled video segments. The code will be available at https://github.com/wenlongli10/VADTree.

Boosting Global-Local Feature Matching via Anomaly Synthesis for Multi-Class Point Cloud Anomaly Detection

Point cloud anomaly detection is essential for various industrial applications. The huge computation and storage costs caused by the increasing product classes limit the application of single-class unsupervised methods, necessitating the development of multi-class unsupervised methods. However, the feature similarity between normal and anomalous points from different class data leads to the feature confusion problem, which greatly hinders the performance of multi-class methods. Therefore, we introduce a multi-class point cloud anomaly detection method, named GLFM, leveraging global-local feature matching to progressively separate data that are prone to confusion across multiple classes. Specifically, GLFM is structured into three stages: Stage-I proposes an anomaly synthesis pipeline that stretches point clouds to create abundant anomaly data that are utilized to adapt the point cloud feature extractor for better feature representation. Stage-II establishes the global and local memory banks according to the global and local feature distributions of all the training data, weakening the impact of feature confusion on the establishment of the memory bank. Stage-III implements anomaly detection of test data leveraging its feature distance from global and local memory banks. Extensive experiments on the MVTec 3D-AD, Real3D-AD and actual industry parts dataset showcase our proposed GLFM's superior point cloud anomaly detection performance. The code is available at https://github.com/hustCYQ/GLFM-Multi-class-3DAD.

A Robust Probability-based Joint Registration Method of Multiple Point Clouds Considering Local Consistency

In robotic inspection, joint registration of multiple point clouds is an essential technique for estimating the transformation relationships between measured parts, such as multiple blades in a propeller. However, the presence of noise and outliers in the data can significantly impair the registration performance by affecting the correctness of correspondences. To address this issue, we incorporate local consistency property into the probability-based joint registration method. Specifically, each measured point set is treated as a sample from an unknown Gaussian Mixture Model (GMM), and the registration problem is framed as estimating the probability model. By incorporating local consistency into the optimization process, we enhance the robustness and accuracy of the posterior distributions, which represent the one-to-all correspondences that directly determine the registration results. Effective closed-form solution for transformation and probability parameters are derived with Expectation-Maximization (EM) algorithm. Extensive experiments demonstrate that our method outperforms the existing methods, achieving high accuracy and robustness with the existence of noise and outliers. The code will be available at https://github.com/sulingjie/JPRLC_registration.

Robust Point Cloud Registration in Robotic Inspection with Locally Consistent Gaussian Mixture Model

In robotic inspection of aviation parts, achieving accurate pairwise point cloud registration between scanned and model data is essential. However, noise and outliers generated in robotic scanned data can compromise registration accuracy. To mitigate this challenge, this article proposes a probability-based registration method utilizing Gaussian Mixture Model (GMM) with local consistency constraint. This method converts the registration problem into a model fitting one, constraining the similarity of posterior distributions between neighboring points to enhance correspondence robustness. We employ the Expectation Maximization algorithm iteratively to find optimal rotation matrix and translation vector while obtaining GMM parameters. Both E-step and M-step have closed-form solutions. Simulation and actual experiments confirm the method's effectiveness, reducing root mean square error by 20% despite the presence of noise and outliers. The proposed method excels in robustness and accuracy compared to existing methods.

Mapping the Empirical Evidence of the GDPR Effectiveness: A Systematic Review

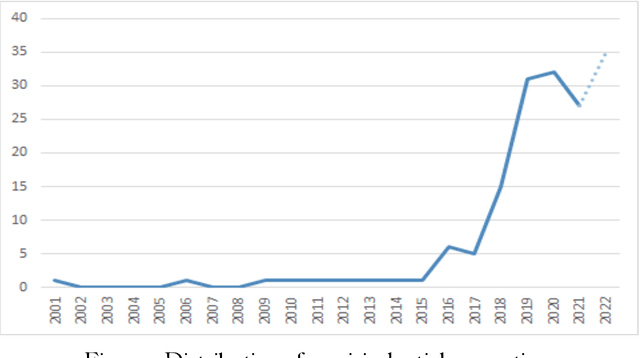
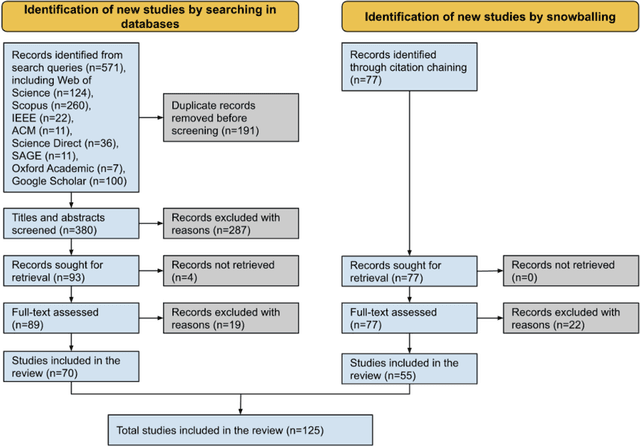
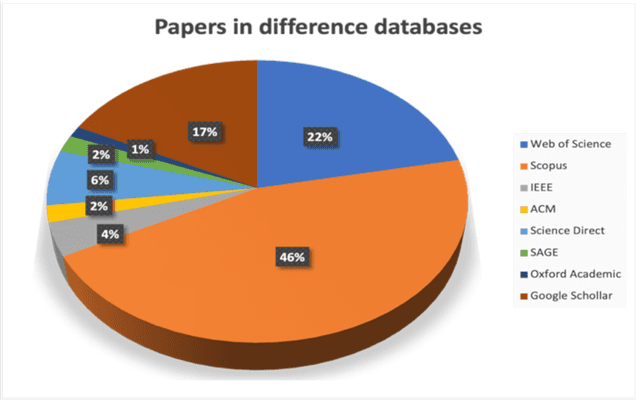
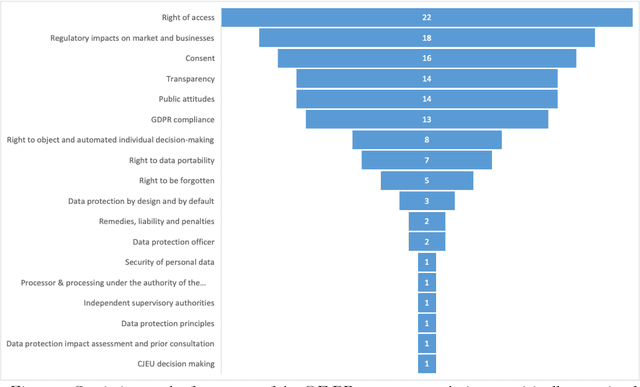
In the realm of data protection, a striking disconnect prevails between traditional domains of doctrinal, legal, theoretical, and policy-based inquiries and a burgeoning body of empirical evidence. Much of the scholarly and regulatory discourse remains entrenched in abstract legal principles or normative frameworks, leaving the empirical landscape uncharted or minimally engaged. Since the birth of EU data protection law, a modest body of empirical evidence has been generated but remains widely scattered and unexamined. Such evidence offers vital insights into the perception, impact, clarity, and effects of data protection measures but languishes on the periphery, inadequately integrated into the broader conversation. To make a meaningful connection, we conduct a comprehensive review and synthesis of empirical research spanning nearly three decades (1995- March 2022), advocating for a more robust integration of empirical evidence into the evaluation and review of the GDPR, while laying a methodological foundation for future empirical research.