Improving Robustness of AlphaZero Algorithms to Test-Time Environment Changes

The AlphaZero framework provides a standard way of combining Monte Carlo planning with prior knowledge provided by a previously trained policy-value neural network. AlphaZero usually assumes that the environment on which the neural network was trained will not change at test time, which constrains its applicability. In this paper, we analyze the problem of deploying AlphaZero agents in potentially changed test environments and demonstrate how the combination of simple modifications to the standard framework can significantly boost performance, even in settings with a low planning budget available. The code is publicly available on GitHub.

Modular Recurrence in Contextual MDPs for Universal Morphology Control

A universal controller for any robot morphology would greatly improve computational and data efficiency. By utilizing contextual information about the properties of individual robots and exploiting their modular structure in the architecture of deep reinforcement learning agents, steps have been made towards multi-robot control. Generalization to new, unseen robots, however, remains a challenge. In this paper we hypothesize that the relevant contextual information is partially observable, but that it can be inferred through interactions for better generalization to contexts that are not seen during training. To this extent, we implement a modular recurrent architecture and evaluate its generalization performance on a large set of MuJoCo robots. The results show a substantial improved performance on robots with unseen dynamics, kinematics, and topologies, in four different environments.

Universal Value-Function Uncertainties

Estimating epistemic uncertainty in value functions is a crucial challenge for many aspects of reinforcement learning (RL), including efficient exploration, safe decision-making, and offline RL. While deep ensembles provide a robust method for quantifying value uncertainty, they come with significant computational overhead. Single-model methods, while computationally favorable, often rely on heuristics and typically require additional propagation mechanisms for myopic uncertainty estimates. In this work we introduce universal value-function uncertainties (UVU), which, similar in spirit to random network distillation (RND), quantify uncertainty as squared prediction errors between an online learner and a fixed, randomly initialized target network. Unlike RND, UVU errors reflect policy-conditional value uncertainty, incorporating the future uncertainties any given policy may encounter. This is due to the training procedure employed in UVU: the online network is trained using temporal difference learning with a synthetic reward derived from the fixed, randomly initialized target network. We provide an extensive theoretical analysis of our approach using neural tangent kernel (NTK) theory and show that in the limit of infinite network width, UVU errors are exactly equivalent to the variance of an ensemble of independent universal value functions. Empirically, we show that UVU achieves equal performance to large ensembles on challenging multi-task offline RL settings, while offering simplicity and substantial computational savings.

How Ensembles of Distilled Policies Improve Generalisation in Reinforcement Learning

In the zero-shot policy transfer setting in reinforcement learning, the goal is to train an agent on a fixed set of training environments so that it can generalise to similar, but unseen, testing environments. Previous work has shown that policy distillation after training can sometimes produce a policy that outperforms the original in the testing environments. However, it is not yet entirely clear why that is, or what data should be used to distil the policy. In this paper, we prove, under certain assumptions, a generalisation bound for policy distillation after training. The theory provides two practical insights: for improved generalisation, you should 1) train an ensemble of distilled policies, and 2) distil it on as much data from the training environments as possible. We empirically verify that these insights hold in more general settings, when the assumptions required for the theory no longer hold. Finally, we demonstrate that an ensemble of policies distilled on a diverse dataset can generalise significantly better than the original agent.

Contextual Similarity Distillation: Ensemble Uncertainties with a Single Model

Uncertainty quantification is a critical aspect of reinforcement learning and deep learning, with numerous applications ranging from efficient exploration and stable offline reinforcement learning to outlier detection in medical diagnostics. The scale of modern neural networks, however, complicates the use of many theoretically well-motivated approaches such as full Bayesian inference. Approximate methods like deep ensembles can provide reliable uncertainty estimates but still remain computationally expensive. In this work, we propose contextual similarity distillation, a novel approach that explicitly estimates the variance of an ensemble of deep neural networks with a single model, without ever learning or evaluating such an ensemble in the first place. Our method builds on the predictable learning dynamics of wide neural networks, governed by the neural tangent kernel, to derive an efficient approximation of the predictive variance of an infinite ensemble. Specifically, we reinterpret the computation of ensemble variance as a supervised regression problem with kernel similarities as regression targets. The resulting model can estimate predictive variance at inference time with a single forward pass, and can make use of unlabeled target-domain data or data augmentations to refine its uncertainty estimates. We empirically validate our method across a variety of out-of-distribution detection benchmarks and sparse-reward reinforcement learning environments. We find that our single-model method performs competitively and sometimes superior to ensemble-based baselines and serves as a reliable signal for efficient exploration. These results, we believe, position contextual similarity distillation as a principled and scalable alternative for uncertainty quantification in reinforcement learning and general deep learning.

Training on more Reachable Tasks for Generalisation in Reinforcement Learning

In multi-task reinforcement learning, agents train on a fixed set of tasks and have to generalise to new ones. Recent work has shown that increased exploration improves this generalisation, but it remains unclear why exactly that is. In this paper, we introduce the concept of reachability in multi-task reinforcement learning and show that an initial exploration phase increases the number of reachable tasks the agent is trained on. This, and not the increased exploration, is responsible for the improved generalisation, even to unreachable tasks. Inspired by this, we propose a novel method Explore-Go that implements such an exploration phase at the beginning of each episode. Explore-Go only modifies the way experience is collected and can be used with most existing on-policy or off-policy reinforcement learning algorithms. We demonstrate the effectiveness of our method when combined with some popular algorithms and show an increase in generalisation performance across several environments.

Explore-Go: Leveraging Exploration for Generalisation in Deep Reinforcement Learning

One of the remaining challenges in reinforcement learning is to develop agents that can generalise to novel scenarios they might encounter once deployed. This challenge is often framed in a multi-task setting where agents train on a fixed set of tasks and have to generalise to new tasks. Recent work has shown that in this setting increased exploration during training can be leveraged to increase the generalisation performance of the agent. This makes sense when the states encountered during testing can actually be explored during training. In this paper, we provide intuition why exploration can also benefit generalisation to states that cannot be explicitly encountered during training. Additionally, we propose a novel method Explore-Go that exploits this intuition by increasing the number of states on which the agent trains. Explore-Go effectively increases the starting state distribution of the agent and as a result can be used in conjunction with most existing on-policy or off-policy reinforcement learning algorithms. We show empirically that our method can increase generalisation performance in an illustrative environment and on the Procgen benchmark.

A Penalty-Based Guardrail Algorithm for Non-Decreasing Optimization with Inequality Constraints

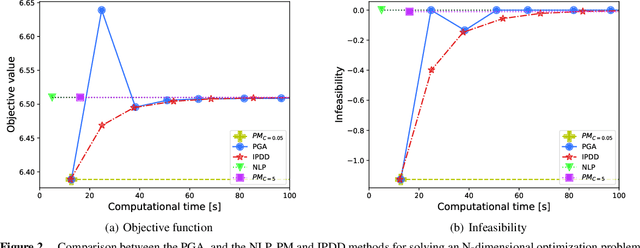
Traditional mathematical programming solvers require long computational times to solve constrained minimization problems of complex and large-scale physical systems. Therefore, these problems are often transformed into unconstrained ones, and solved with computationally efficient optimization approaches based on first-order information, such as the gradient descent method. However, for unconstrained problems, balancing the minimization of the objective function with the reduction of constraint violations is challenging. We consider the class of time-dependent minimization problems with increasing (possibly) nonlinear and non-convex objective function and non-decreasing (possibly) nonlinear and non-convex inequality constraints. To efficiently solve them, we propose a penalty-based guardrail algorithm (PGA). This algorithm adapts a standard penalty-based method by dynamically updating the right-hand side of the constraints with a guardrail variable which adds a margin to prevent violations. We evaluate PGA on two novel application domains: a simplified model of a district heating system and an optimization model derived from learned deep neural networks. Our method significantly outperforms mathematical programming solvers and the standard penalty-based method, and achieves better performance and faster convergence than a state-of-the-art algorithm (IPDD) within a specified time limit.

To the Max: Reinventing Reward in Reinforcement Learning

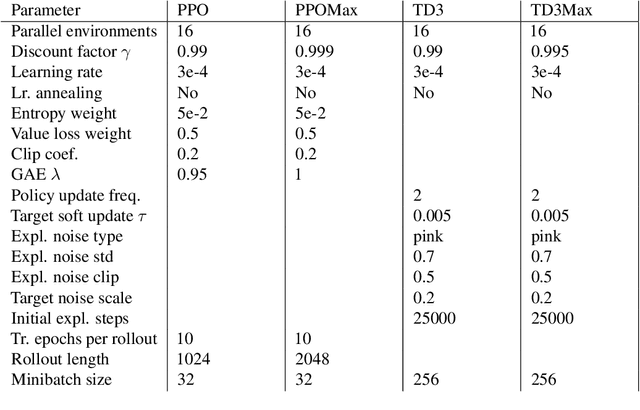
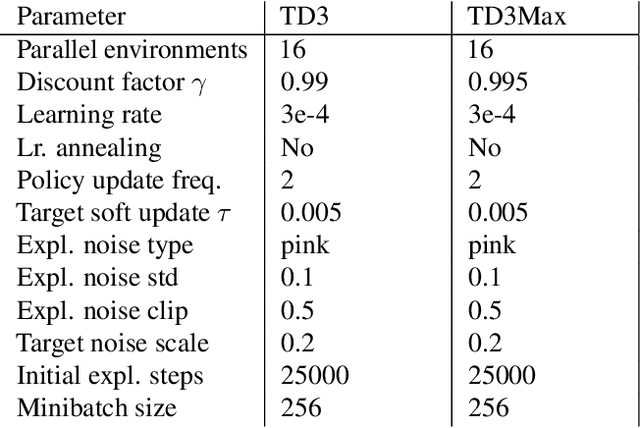
In reinforcement learning (RL), different rewards can define the same optimal policy but result in drastically different learning performance. For some, the agent gets stuck with a suboptimal behavior, and for others, it solves the task efficiently. Choosing a good reward function is hence an extremely important yet challenging problem. In this paper, we explore an alternative approach to using rewards for learning. We introduce max-reward RL, where an agent optimizes the maximum rather than the cumulative reward. Unlike earlier works, our approach works for deterministic and stochastic environments and can be easily combined with state-of-the-art RL algorithms. In the experiments, we study the performance of max-reward RL algorithms in two goal-reaching environments from Gymnasium-Robotics and demonstrate its benefits over standard RL. The code is publicly available.

Multi-Robot Local Motion Planning Using Dynamic Optimization Fabrics

In this paper, we address the problem of real-time motion planning for multiple robotic manipulators that operate in close proximity. We build upon the concept of dynamic fabrics and extend them to multi-robot systems, referred to as Multi-Robot Dynamic Fabrics (MRDF). This geometric method enables a very high planning frequency for high-dimensional systems at the expense of being reactive and prone to deadlocks. To detect and resolve deadlocks, we propose Rollout Fabrics where MRDF are forward simulated in a decentralized manner. We validate the methods in simulated close-proximity pick-and-place scenarios with multiple manipulators, showing high success rates and real-time performance.