A Penalty-Based Guardrail Algorithm for Non-Decreasing Optimization with Inequality Constraints
Paper and Code
May 03, 2024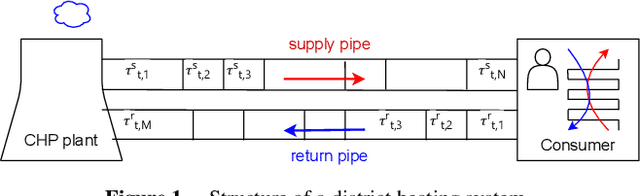


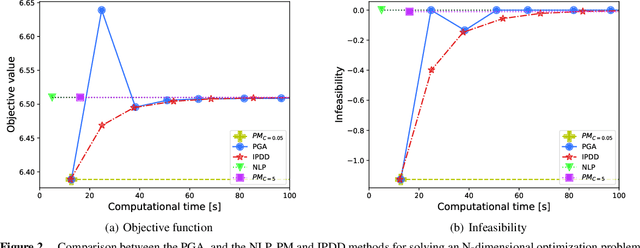
Traditional mathematical programming solvers require long computational times to solve constrained minimization problems of complex and large-scale physical systems. Therefore, these problems are often transformed into unconstrained ones, and solved with computationally efficient optimization approaches based on first-order information, such as the gradient descent method. However, for unconstrained problems, balancing the minimization of the objective function with the reduction of constraint violations is challenging. We consider the class of time-dependent minimization problems with increasing (possibly) nonlinear and non-convex objective function and non-decreasing (possibly) nonlinear and non-convex inequality constraints. To efficiently solve them, we propose a penalty-based guardrail algorithm (PGA). This algorithm adapts a standard penalty-based method by dynamically updating the right-hand side of the constraints with a guardrail variable which adds a margin to prevent violations. We evaluate PGA on two novel application domains: a simplified model of a district heating system and an optimization model derived from learned deep neural networks. Our method significantly outperforms mathematical programming solvers and the standard penalty-based method, and achieves better performance and faster convergence than a state-of-the-art algorithm (IPDD) within a specified time limit.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge