Weiyan Chen
Convolutional Sparse Coding for Compressed Sensing CT Reconstruction
Mar 20, 2019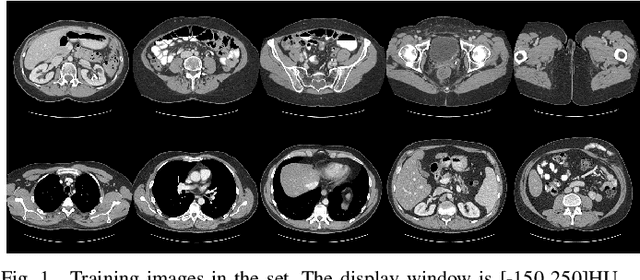
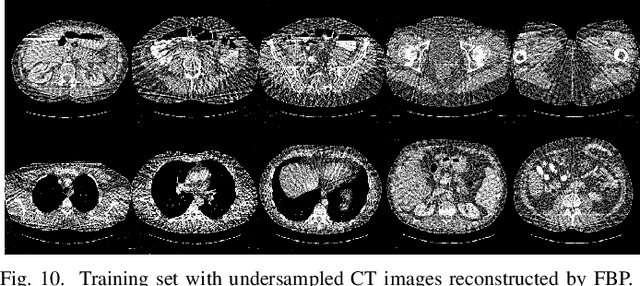


Abstract:Over the past few years, dictionary learning (DL)-based methods have been successfully used in various image reconstruction problems. However, traditional DL-based computed tomography (CT) reconstruction methods are patch-based and ignore the consistency of pixels in overlapped patches. In addition, the features learned by these methods always contain shifted versions of the same features. In recent years, convolutional sparse coding (CSC) has been developed to address these problems. In this paper, inspired by several successful applications of CSC in the field of signal processing, we explore the potential of CSC in sparse-view CT reconstruction. By directly working on the whole image, without the necessity of dividing the image into overlapped patches in DL-based methods, the proposed methods can maintain more details and avoid artifacts caused by patch aggregation. With predetermined filters, an alternating scheme is developed to optimize the objective function. Extensive experiments with simulated and real CT data were performed to validate the effectiveness of the proposed methods. Qualitative and quantitative results demonstrate that the proposed methods achieve better performance than several existing state-of-the-art methods.
Optimal control with reset-renewable resources
Sep 27, 2014



Abstract:We consider both discrete and continuous control problems constrained by a fixed budget of some resource, which may be renewed upon entering a preferred subset of the state space. In the discrete case, we consider both deterministic and stochastic shortest path problems with full budget resets in all preferred nodes. In the continuous case, we derive augmented PDEs of optimal control, which are then solved numerically on the extended state space with a full/instantaneous budget reset on the preferred subset. We introduce an iterative algorithm for solving these problems efficiently. The method's performance is demonstrated on a range of computational examples, including the optimal path planning with constraints on prolonged visibility by a static enemy observer. In addition, we also develop an algorithm that works on the original state space to solve a related but simpler problem: finding the subsets of the domain "reachable-within-the-budget". This manuscript is an extended version of the paper accepted for publication by SIAM J. on Control and Optimization. In the journal version, Section 3 and the Appendix were omitted due to space limitations.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge