Multiple penalized principal curves: analysis and computation

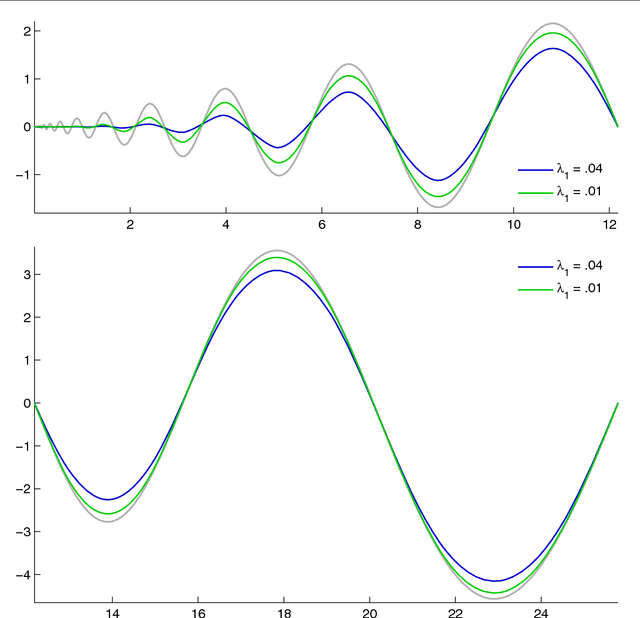
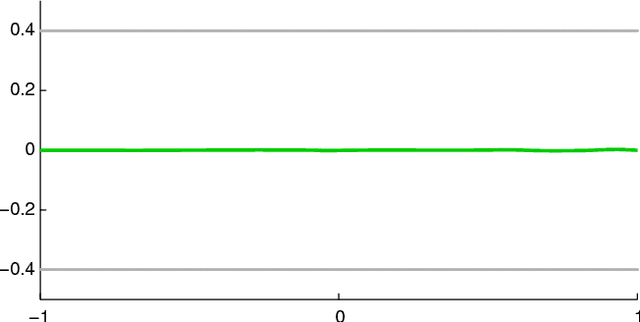
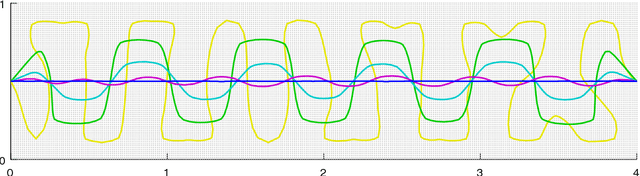
We study the problem of finding the one-dimensional structure in a given data set. In other words we consider ways to approximate a given measure (data) by curves. We consider an objective functional whose minimizers are a regularization of principal curves and introduce a new functional which allows for multiple curves. We prove the existence of minimizers and establish their basic properties. We develop an efficient algorithm for obtaining (near) minimizers of the functional. While both of the functionals used are nonconvex, we argue that enlarging the configuration space to allow for multiple curves leads to a simpler energy landscape with fewer undesirable (high-energy) local minima. Furthermore we note that the approach proposed is able to find the one-dimensional structure even for data with considerable amount of noise.

Optimal control with reset-renewable resources

We consider both discrete and continuous control problems constrained by a fixed budget of some resource, which may be renewed upon entering a preferred subset of the state space. In the discrete case, we consider both deterministic and stochastic shortest path problems with full budget resets in all preferred nodes. In the continuous case, we derive augmented PDEs of optimal control, which are then solved numerically on the extended state space with a full/instantaneous budget reset on the preferred subset. We introduce an iterative algorithm for solving these problems efficiently. The method's performance is demonstrated on a range of computational examples, including the optimal path planning with constraints on prolonged visibility by a static enemy observer. In addition, we also develop an algorithm that works on the original state space to solve a related but simpler problem: finding the subsets of the domain "reachable-within-the-budget". This manuscript is an extended version of the paper accepted for publication by SIAM J. on Control and Optimization. In the journal version, Section 3 and the Appendix were omitted due to space limitations.