A bi-criteria path planning algorithm for robotics applications

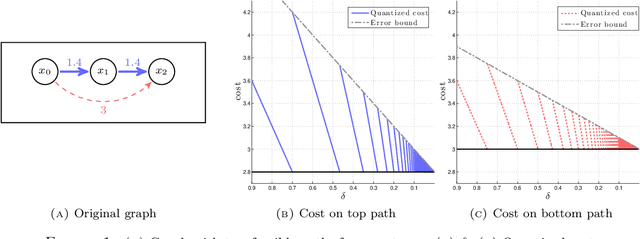
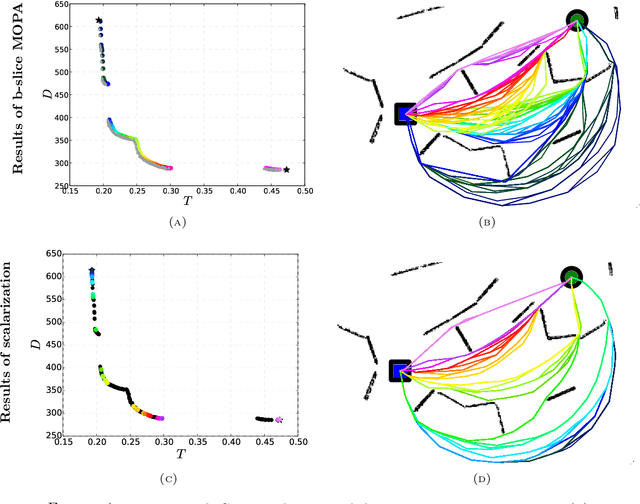
Realistic path planning applications often require optimizing with respect to several criteria simultaneously. Here we introduce an efficient algorithm for bi-criteria path planning on graphs. Our approach is based on augmenting the state space to keep track of the "budget" remaining to satisfy the constraints on secondary cost. The resulting augmented graph is acyclic and the primary cost can be then minimized by a simple upward sweep through budget levels. The efficiency and accuracy of our algorithm is tested on Probabilistic Roadmap graphs to minimize the distance of travel subject to a constraint on the overall threat exposure of the robot. We also present the results from field experiments illustrating the use of this approach on realistic robotic systems.

Optimal control with reset-renewable resources

We consider both discrete and continuous control problems constrained by a fixed budget of some resource, which may be renewed upon entering a preferred subset of the state space. In the discrete case, we consider both deterministic and stochastic shortest path problems with full budget resets in all preferred nodes. In the continuous case, we derive augmented PDEs of optimal control, which are then solved numerically on the extended state space with a full/instantaneous budget reset on the preferred subset. We introduce an iterative algorithm for solving these problems efficiently. The method's performance is demonstrated on a range of computational examples, including the optimal path planning with constraints on prolonged visibility by a static enemy observer. In addition, we also develop an algorithm that works on the original state space to solve a related but simpler problem: finding the subsets of the domain "reachable-within-the-budget". This manuscript is an extended version of the paper accepted for publication by SIAM J. on Control and Optimization. In the journal version, Section 3 and the Appendix were omitted due to space limitations.