Multiple penalized principal curves: analysis and computation
Paper and Code
Aug 30, 2016
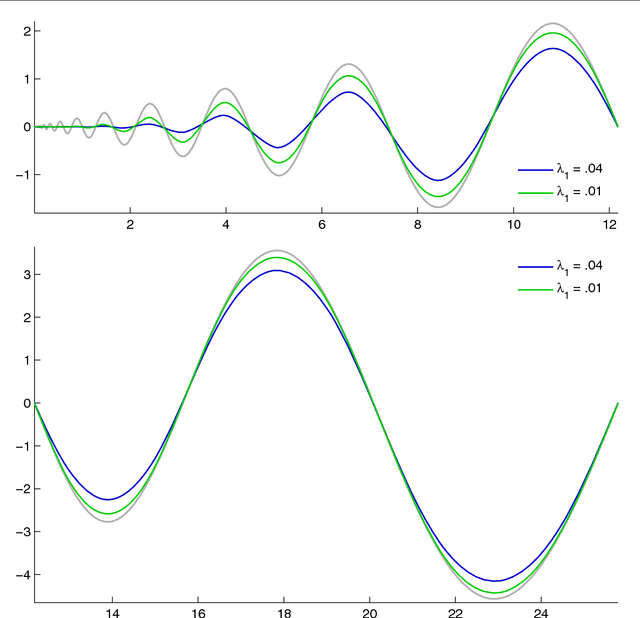
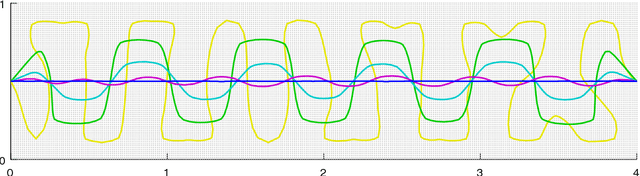
We study the problem of finding the one-dimensional structure in a given data set. In other words we consider ways to approximate a given measure (data) by curves. We consider an objective functional whose minimizers are a regularization of principal curves and introduce a new functional which allows for multiple curves. We prove the existence of minimizers and establish their basic properties. We develop an efficient algorithm for obtaining (near) minimizers of the functional. While both of the functionals used are nonconvex, we argue that enlarging the configuration space to allow for multiple curves leads to a simpler energy landscape with fewer undesirable (high-energy) local minima. Furthermore we note that the approach proposed is able to find the one-dimensional structure even for data with considerable amount of noise.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge