PRIMP: PRobabilistically-Informed Motion Primitives for Efficient Affordance Learning from Demonstration

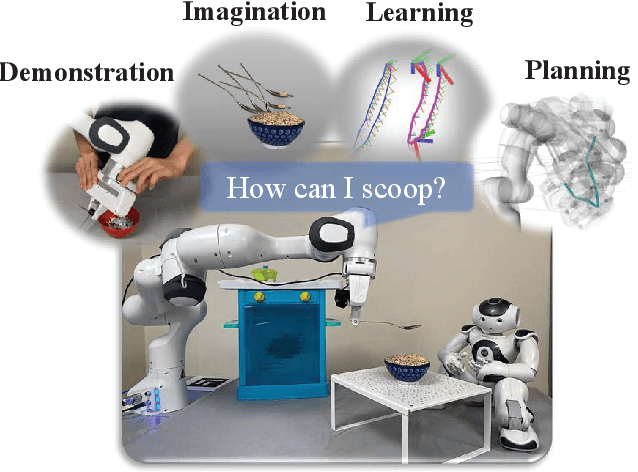
This paper proposes a learning-from-demonstration method using probability densities on the workspaces of robot manipulators. The method, named "PRobabilistically-Informed Motion Primitives (PRIMP)", learns the probability distribution of the end effector trajectories in the 6D workspace that includes both positions and orientations. It is able to adapt to new situations such as novel via poses with uncertainty and a change of viewing frame. The method itself is robot-agnostic, in which the learned distribution can be transferred to another robot with the adaptation to its workspace density. The learned trajectory distribution is then used to guide an optimization-based motion planning algorithm to further help the robot avoid novel obstacles that are unseen during the demonstration process. The proposed methods are evaluated by several sets of benchmark experiments. PRIMP runs more than 5 times faster while generalizing trajectories more than twice as close to both the demonstrations and novel desired poses. It is then combined with our robot imagination method that learns object affordances, illustrating the applicability of PRIMP to learn tool use through physical experiments.

Learning-Free Grasping of Unknown Objects Using Hidden Superquadrics

Robotic grasping is an essential and fundamental task and has been studied extensively over the past several decades. Traditional work analyzes physical models of the objects and computes force-closure grasps. Such methods require pre-knowledge of the complete 3D model of an object, which can be hard to obtain. Recently with significant progress in machine learning, data-driven methods have dominated the area. Although impressive improvements have been achieved, those methods require a vast amount of training data and suffer from limited generalizability. In this paper, we propose a novel two-stage approach to predicting and synthesizing grasping poses directly from the point cloud of an object without database knowledge or learning. Firstly, multiple superquadrics are recovered at different positions within the object, representing the local geometric features of the object surface. Subsequently, our algorithm exploits the tri-symmetry feature of superquadrics and synthesizes a list of antipodal grasps from each recovered superquadric. An evaluation model is designed to assess and quantify the quality of each grasp candidate. The grasp candidate with the highest score is then selected as the final grasping pose. We conduct experiments on isolated and packed scenes to corroborate the effectiveness of our method. The results indicate that our method demonstrates competitive performance compared with the state-of-the-art without the need for either a full model or prior training.

Marching-Primitives: Shape Abstraction from Signed Distance Function

Representing complex objects with basic geometric primitives has long been a topic in computer vision. Primitive-based representations have the merits of compactness and computational efficiency in higher-level tasks such as physics simulation, collision checking, and robotic manipulation. Unlike previous works which extract polygonal meshes from a signed distance function (SDF), in this paper, we present a novel method, named Marching-Primitives, to obtain a primitive-based abstraction directly from an SDF. Our method grows geometric primitives (such as superquadrics) iteratively by analyzing the connectivity of voxels while marching at different levels of signed distance. For each valid connected volume of interest, we march on the scope of voxels from which a primitive is able to be extracted in a probabilistic sense and simultaneously solve for the parameters of the primitive to capture the underlying local geometry. We evaluate the performance of our method on both synthetic and real-world datasets. The results show that the proposed method outperforms the state-of-the-art in terms of accuracy, and is directly generalizable among different categories and scales. The code is open-sourced at https://github.com/ChirikjianLab/Marching-Primitives.git.

Primitive-based Shape Abstraction via Nonparametric Bayesian Inference

3D shape abstraction has drawn great interest over the years. Apart from low-level representations such as meshes and voxels, researchers also seek to semantically abstract complex objects with basic geometric primitives. Recent deep learning methods rely heavily on datasets, with limited generality to unseen categories. Furthermore, abstracting an object accurately yet with a small number of primitives still remains a challenge. In this paper, we propose a novel non-parametric Bayesian statistical method to infer an abstraction, consisting of an unknown number of geometric primitives, from a point cloud. We model the generation of points as observations sampled from an infinite mixture of Gaussian Superquadric Taper Models (GSTM). Our approach formulates the abstraction as a clustering problem, in which: 1) each point is assigned to a cluster via the Chinese Restaurant Process (CRP); 2) a primitive representation is optimized for each cluster, and 3) a merging post-process is incorporated to provide a concise representation. We conduct extensive experiments on various datasets. The results indicate that our method outperforms the state-of-the-art in terms of accuracy and is generalizable to various types of objects.

Robust and Accurate Superquadric Recovery: a Probabilistic Approach

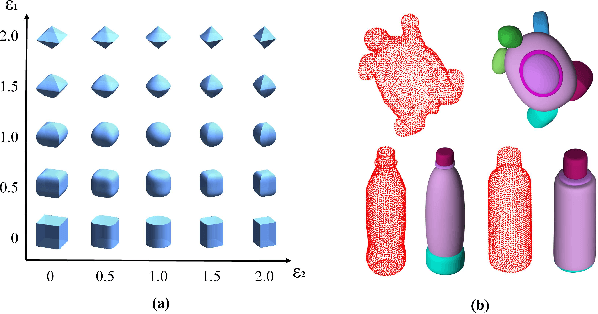
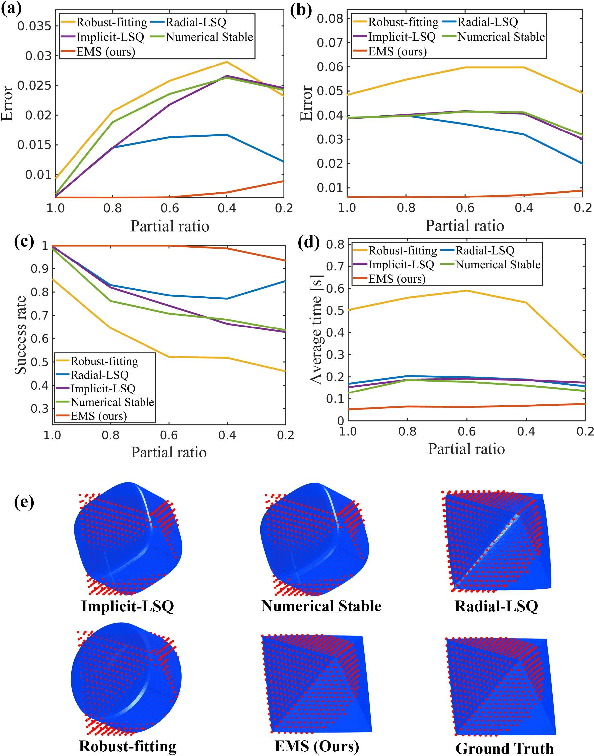
Interpreting objects with basic geometric primitives has long been studied in computer vision. Among geometric primitives, superquadrics are well known for their simple implicit expressions and capability of representing a wide range of shapes with few parameters. However, as the first and foremost step, recovering superquadrics accurately and robustly from 3D data still remains challenging. The existing methods are subject to local optima and are sensitive to noise and outliers in real-world scenarios, resulting in frequent failure in capturing geometric shapes. In this paper, we propose the first probabilistic method to recover superquadrics from point clouds. Our method builds a Gaussian-uniform mixture model (GUM) on the parametric surface of a superquadric, which explicitly models the generation of outliers and noise. The superquadric recovery is formulated as a Maximum Likelihood Estimation (MLE) problem. We propose an algorithm, Expectation, Maximization, and Switching (EMS), to solve this problem, where: (1) outliers are predicted from the posterior perspective; (2) the superquadric parameter is optimized by the trust-region reflective algorithm; and (3) local optima are avoided by globally searching and switching among parameters encoding similar superquadrics. We show that our method can be extended to the multi-superquadrics recovery for complex objects. The proposed method outperforms the state-of-the-art in terms of accuracy, efficiency, and robustness on both synthetic and real-world datasets. Codes will be released.

LSG-CPD: Coherent Point Drift with Local Surface Geometry for Point Cloud Registration

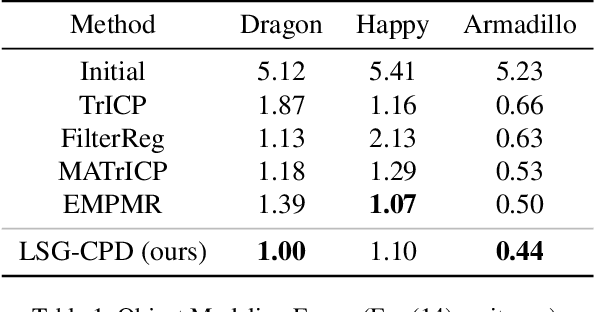
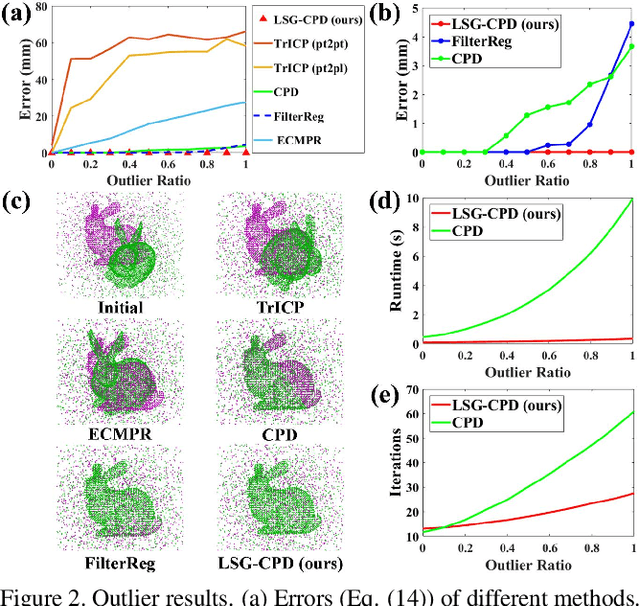
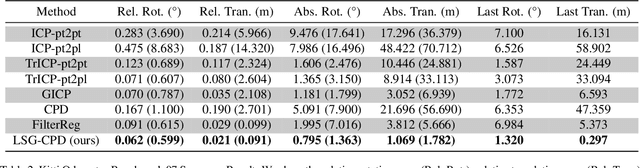
Probabilistic point cloud registration methods are becoming more popular because of their robustness. However, unlike point-to-plane variants of iterative closest point (ICP) which incorporate local surface geometric information such as surface normals, most probabilistic methods (e.g., coherent point drift (CPD)) ignore such information and build Gaussian mixture models (GMMs) with isotropic Gaussian covariances. This results in sphere-like GMM components which only penalize the point-to-point distance between the two point clouds. In this paper, we propose a novel method called CPD with Local Surface Geometry (LSG-CPD) for rigid point cloud registration. Our method adaptively adds different levels of point-to-plane penalization on top of the point-to-point penalization based on the flatness of the local surface. This results in GMM components with anisotropic covariances. We formulate point cloud registration as a maximum likelihood estimation (MLE) problem and solve it with the Expectation-Maximization (EM) algorithm. In the E step, we demonstrate that the computation can be recast into simple matrix manipulations and efficiently computed on a GPU. In the M step, we perform an unconstrained optimization on a matrix Lie group to efficiently update the rigid transformation of the registration. The proposed method outperforms state-of-the-art algorithms in terms of accuracy and robustness on various datasets captured with range scanners, RGBD cameras, and LiDARs. Also, it is significantly faster than modern implementations of CPD. The code will be released.