Variable Substitution and Bilinear Programming for Aligning Partially Overlapping Point Sets

In many applications, the demand arises for algorithms capable of aligning partially overlapping point sets while remaining invariant to the corresponding transformations. This research presents a method designed to meet such requirements through minimization of the objective function of the robust point matching (RPM) algorithm. First, we show that the RPM objective is a cubic polynomial. Then, through variable substitution, we transform the RPM objective to a quadratic function. Leveraging the convex envelope of bilinear monomials, we proceed to relax the resulting objective function, thus obtaining a lower bound problem that can be conveniently decomposed into distinct linear assignment and low-dimensional convex quadratic program components, both amenable to efficient optimization. Furthermore, a branch-and-bound (BnB) algorithm is devised, which solely branches over the transformation parameters, thereby boosting convergence rate. Empirical evaluations demonstrate better robustness of the proposed methodology against non-rigid deformation, positional noise, and outliers, particularly in scenarios where outliers remain distinct from inliers, when compared with prevailing state-of-the-art approaches.

Hybrid Trilinear and Bilinear Programming for Aligning Partially Overlapping Point Sets

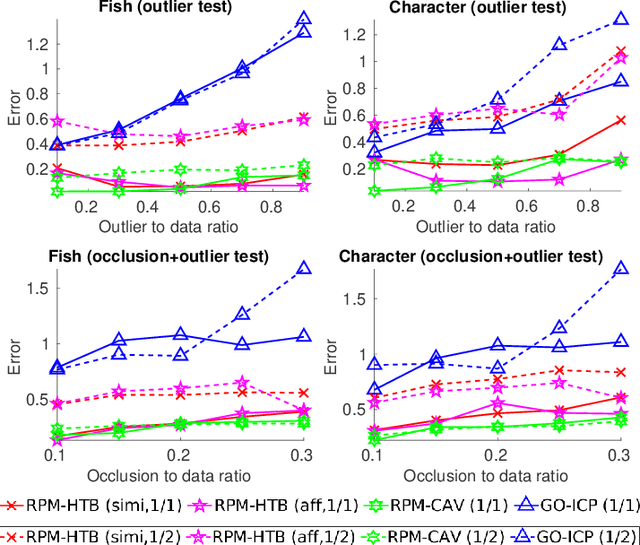
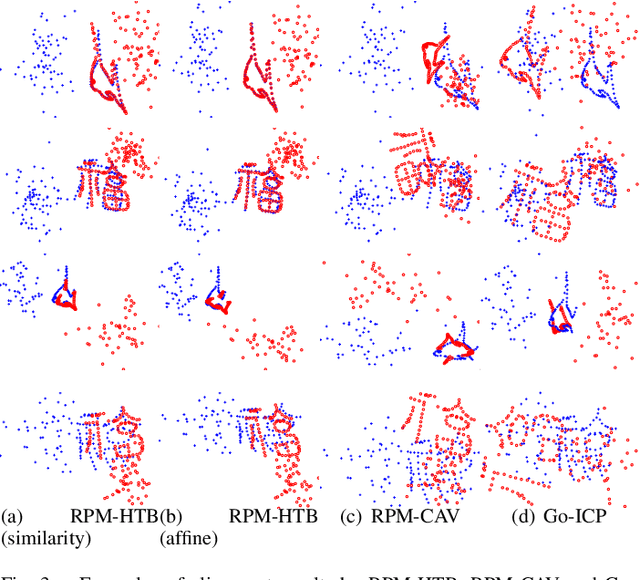
Alignment methods which can handle partially overlapping point sets and are invariant to the corresponding transformations are desirable in computer vision, with applications such as providing initial transformation configuration for local search based methods like ICP. To this end, we first show that the objective of the robust point matching (RPM) algorithm is a cubic polynomial. We then utilize the convex envelopes of trilinear and bilinear monomials to develop its lower bounding function. The resulting lower bounding problem can be efficiently solved via linear assignment and low dimensional convex quadratic programming. We next develop a branch-and-bound (BnB) algorithm which only branches over the transformation parameters and converges quickly. Experimental results demonstrated favorable performance of the proposed method over the state-of-the-art methods in terms of robustness and speed.

Aligning Partially Overlapping Point Sets: an Inner Approximation Algorithm

Aligning partially overlapping point sets where there is no prior information about the value of the transformation is a challenging problem in computer vision. To achieve this goal, we first reduce the objective of the robust point matching algorithm to a function of a low dimensional variable. The resulting function, however, is only concave over a finite region including the feasible region. To cope with this issue, we employ the inner approximation optimization algorithm which only operates within the region where the objective function is concave. Our algorithm does not need regularization on transformation, and thus can handle the situation where there is no prior information about the values of the transformations. Our method is also $\epsilon-$globally optimal and thus is guaranteed to be robust. Moreover, its most computationally expensive subroutine is a linear assignment problem which can be efficiently solved. Experimental results demonstrate the better robustness of the proposed method over state-of-the-art algorithms. Our method is also efficient when the number of transformation parameters is small.

Multi-level Wavelet Convolutional Neural Networks

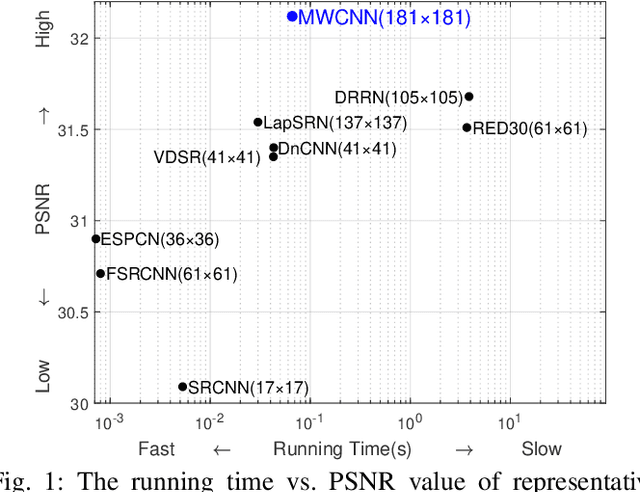
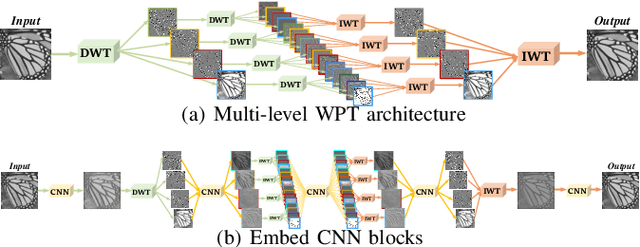
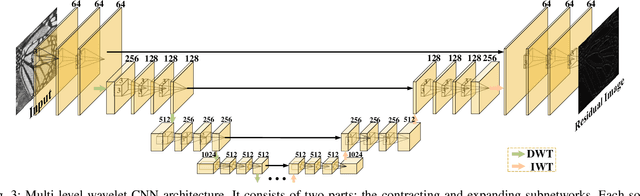
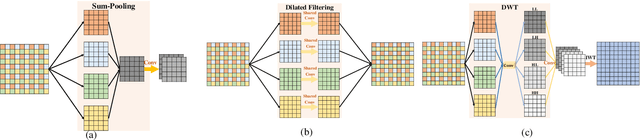
In computer vision, convolutional networks (CNNs) often adopts pooling to enlarge receptive field which has the advantage of low computational complexity. However, pooling can cause information loss and thus is detrimental to further operations such as features extraction and analysis. Recently, dilated filter has been proposed to trade off between receptive field size and efficiency. But the accompanying gridding effect can cause a sparse sampling of input images with checkerboard patterns. To address this problem, in this paper, we propose a novel multi-level wavelet CNN (MWCNN) model to achieve better trade-off between receptive field size and computational efficiency. The core idea is to embed wavelet transform into CNN architecture to reduce the resolution of feature maps while at the same time, increasing receptive field. Specifically, MWCNN for image restoration is based on U-Net architecture, and inverse wavelet transform (IWT) is deployed to reconstruct the high resolution (HR) feature maps. The proposed MWCNN can also be viewed as an improvement of dilated filter and a generalization of average pooling, and can be applied to not only image restoration tasks, but also any CNNs requiring a pooling operation. The experimental results demonstrate effectiveness of the proposed MWCNN for tasks such as image denoising, single image super-resolution, JPEG image artifacts removal and object classification.

Path-following based Point Matching using Similarity Transformation

To address the problem of 3D point matching where the poses of two point sets are unknown, we adapt a recently proposed path following based method to use similarity transformation instead of the original affine transformation. The reduced number of transformation parameters leads to more constrained and desirable matching results. Experimental results demonstrate better robustness of the proposed method over state-of-the-art methods.

A Concave Optimization Algorithm for Matching Partially Overlapping Point Sets

Point matching refers to the process of finding spatial transformation and correspondences between two sets of points. In this paper, we focus on the case that there is only partial overlap between two point sets. Following the approach of the robust point matching method, we model point matching as a mixed linear assignment-least square problem and show that after eliminating the transformation variable, the resulting problem of minimization with respect to point correspondence is a concave optimization problem. Furthermore, this problem has the property that the objective function can be converted into a form with few nonlinear terms via a linear transformation. Based on these properties, we employ the branch-and-bound (BnB) algorithm to optimize the resulting problem where the dimension of the search space is small. To further improve efficiency of the BnB algorithm where computation of the lower bound is the bottleneck, we propose a new lower bounding scheme which has a k-cardinality linear assignment formulation and can be efficiently solved. Experimental results show that the proposed algorithm outperforms state-of-the-art methods in terms of robustness to disturbances and point matching accuracy.