Hybrid Trilinear and Bilinear Programming for Aligning Partially Overlapping Point Sets
Paper and Code
Jan 25, 2021
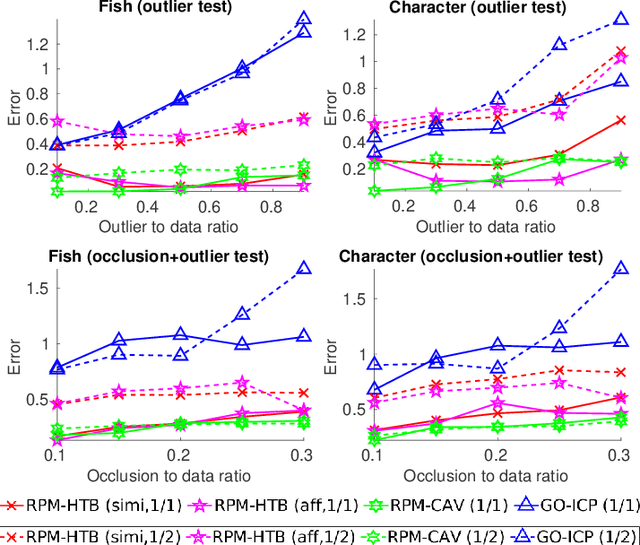
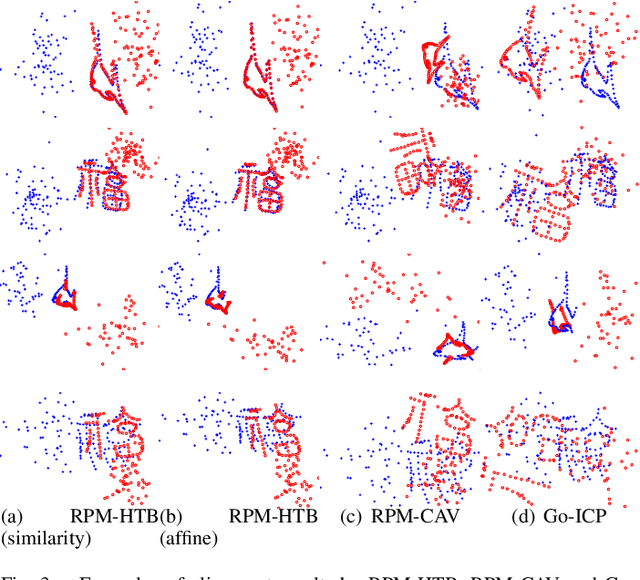

Alignment methods which can handle partially overlapping point sets and are invariant to the corresponding transformations are desirable in computer vision, with applications such as providing initial transformation configuration for local search based methods like ICP. To this end, we first show that the objective of the robust point matching (RPM) algorithm is a cubic polynomial. We then utilize the convex envelopes of trilinear and bilinear monomials to develop its lower bounding function. The resulting lower bounding problem can be efficiently solved via linear assignment and low dimensional convex quadratic programming. We next develop a branch-and-bound (BnB) algorithm which only branches over the transformation parameters and converges quickly. Experimental results demonstrated favorable performance of the proposed method over the state-of-the-art methods in terms of robustness and speed.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge