TRACE: Early Detection of Chronic Kidney Disease Onset with Transformer-Enhanced Feature Embedding

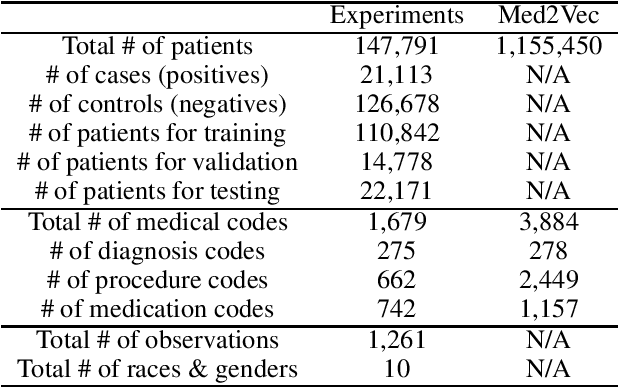
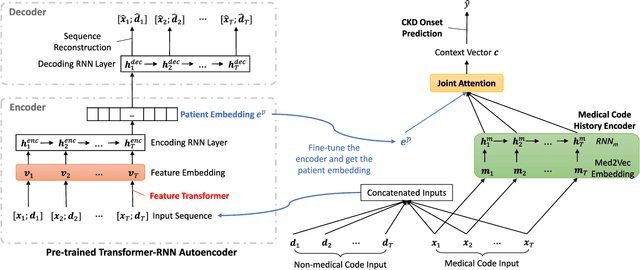
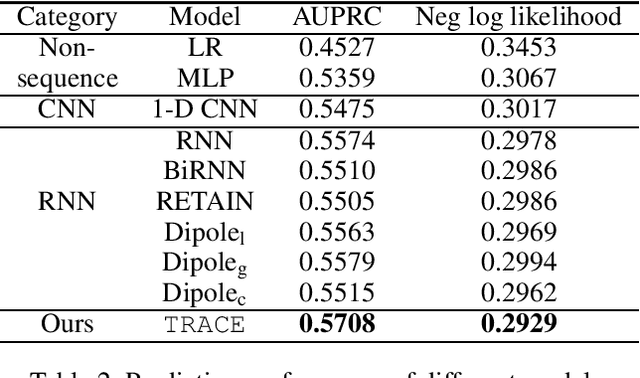
Chronic kidney disease (CKD) has a poor prognosis due to excessive risk factors and comorbidities associated with it. The early detection of CKD faces challenges of insufficient medical histories of positive patients and complicated risk factors. In this paper, we propose the TRACE (Transformer-RNN Autoencoder-enhanced CKD Detector) framework, an end-to-end prediction model using patients' medical history data, to deal with these challenges. TRACE presents a comprehensive medical history representation with a novel key component: a Transformer-RNN autoencoder. The autoencoder jointly learns a medical concept embedding via Transformer for each hospital visit, and a latent representation which summarizes a patient's medical history across all the visits. We compared TRACE with multiple state-of-the-art methods on a dataset derived from real-world medical records. Our model has achieved 0.5708 AUPRC with a 2.31% relative improvement over the best-performing method. We also validated the clinical meaning of the learned embeddings through visualizations and a case study, showing the potential of TRACE to serve as a general disease prediction model.

Identifying Risk of Opioid Use Disorder for Patients Taking Opioid Medications with Deep Learning

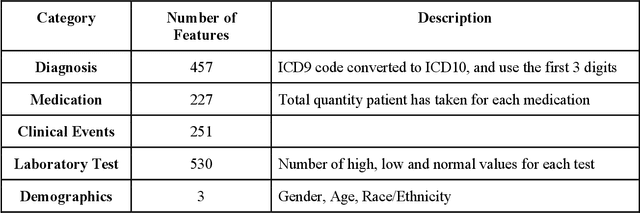
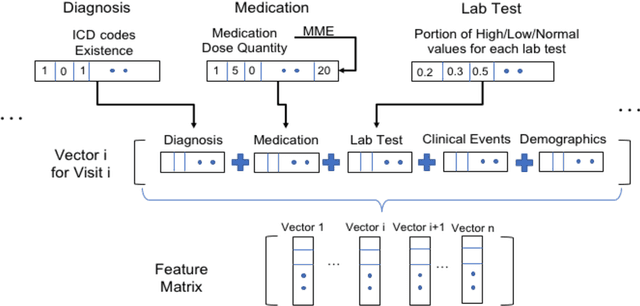
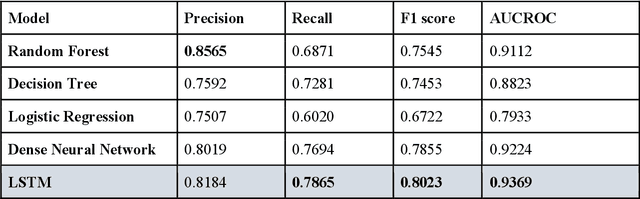
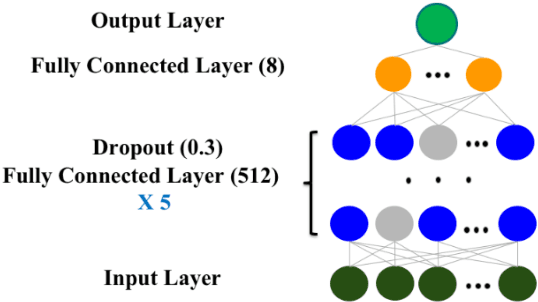
The United States is experiencing an opioid epidemic, and there were more than 10 million opioid misusers aged 12 or older each year. Identifying patients at high risk of Opioid Use Disorder (OUD) can help to make early clinical interventions to reduce the risk of OUD. Our goal is to predict OUD patients among opioid prescription users through analyzing electronic health records with machine learning and deep learning methods. This will help us to better understand the diagnoses of OUD, providing new insights on opioid epidemic. Electronic health records of patients who have been prescribed with medications containing active opioid ingredients were extracted from Cerner Health Facts database between January 1, 2008 and December 31, 2017. Long Short-Term Memory (LSTM) models were applied to predict opioid use disorder risk in the future based on recent five encounters, and compared to Logistic Regression, Random Forest, Decision Tree and Dense Neural Network. Prediction performance was assessed using F-1 score, precision, recall, and AUROC. Our temporal deep learning model provided promising prediction results which outperformed other methods, with a F1 score of 0.8023 and AUCROC of 0.9369. The model can identify OUD related medications and vital signs as important features for the prediction. LSTM based temporal deep learning model is effective on predicting opioid use disorder using a patient past history of electronic health records, with minimal domain knowledge. It has potential to improve clinical decision support for early intervention and prevention to combat the opioid epidemic.

Mixed Strategy May Outperform Pure Strategy: An Initial Study

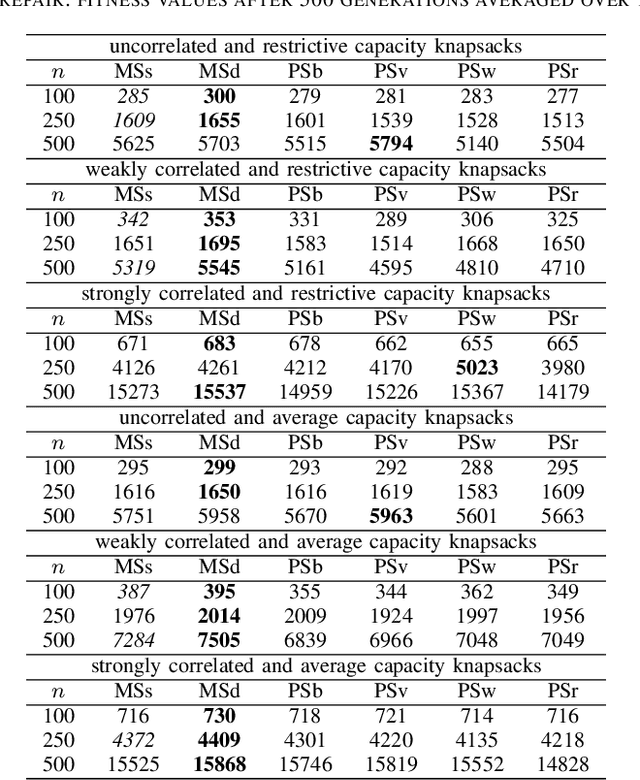
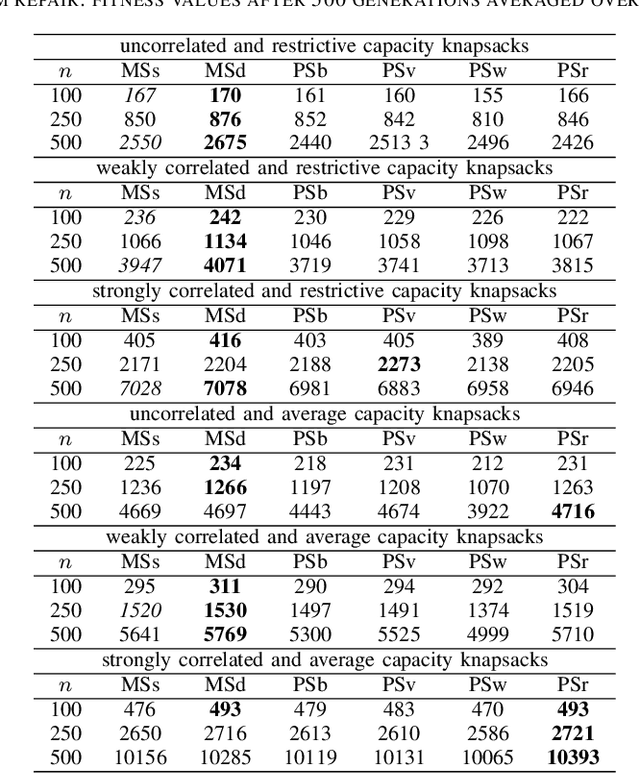
In pure strategy meta-heuristics, only one search strategy is applied for all time. In mixed strategy meta-heuristics, each time one search strategy is chosen from a strategy pool with a probability and then is applied. An example is classical genetic algorithms, where either a mutation or crossover operator is chosen with a probability each time. The aim of this paper is to compare the performance between mixed strategy and pure strategy meta-heuristic algorithms. First an experimental study is implemented and results demonstrate that mixed strategy evolutionary algorithms may outperform pure strategy evolutionary algorithms on the 0-1 knapsack problem in up to 77.8% instances. Then Complementary Strategy Theorem is rigorously proven for applying mixed strategy at the population level. The theorem asserts that given two meta-heuristic algorithms where one uses pure strategy 1 and another uses pure strategy 2, the condition of pure strategy 2 being complementary to pure strategy 1 is sufficient and necessary if there exists a mixed strategy meta-heuristics derived from these two pure strategies and its expected number of generations to find an optimal solution is no more than that of using pure strategy 1 for any initial population, and less than that of using pure strategy 1 for some initial population.