Mixed Strategy May Outperform Pure Strategy: An Initial Study

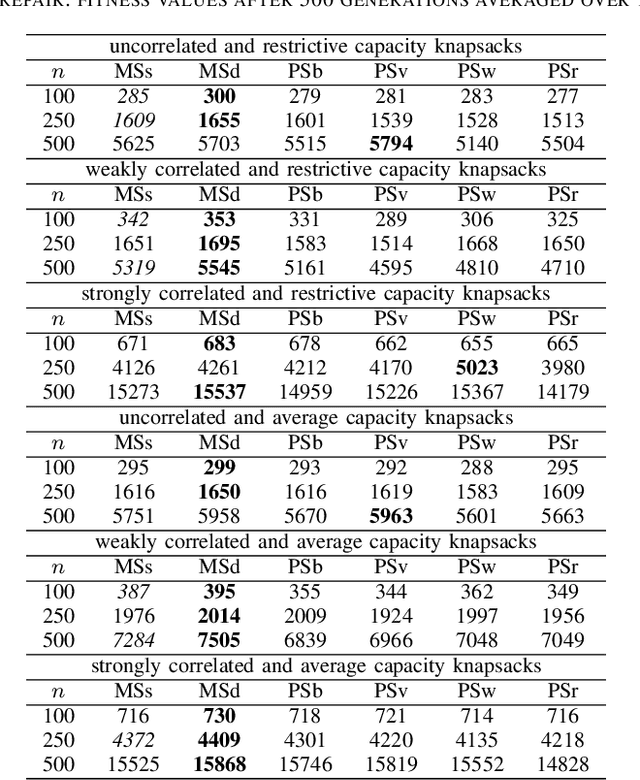
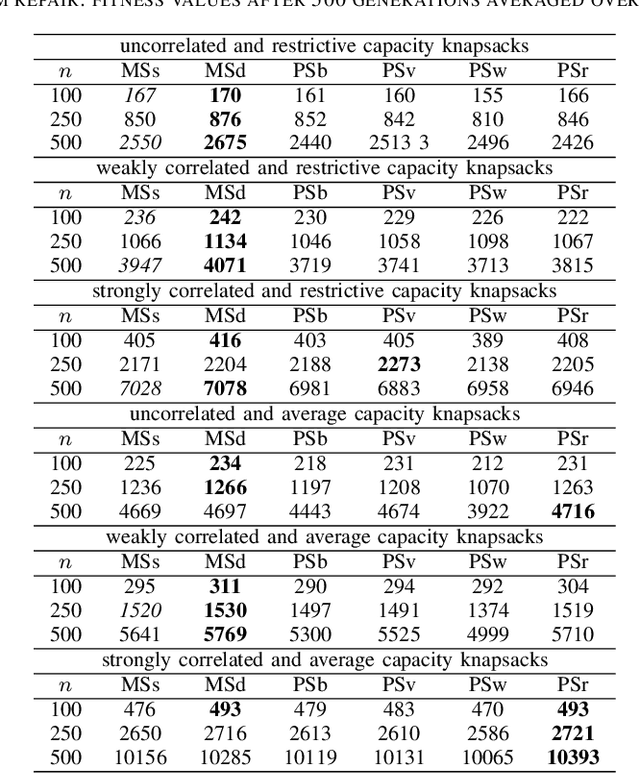
In pure strategy meta-heuristics, only one search strategy is applied for all time. In mixed strategy meta-heuristics, each time one search strategy is chosen from a strategy pool with a probability and then is applied. An example is classical genetic algorithms, where either a mutation or crossover operator is chosen with a probability each time. The aim of this paper is to compare the performance between mixed strategy and pure strategy meta-heuristic algorithms. First an experimental study is implemented and results demonstrate that mixed strategy evolutionary algorithms may outperform pure strategy evolutionary algorithms on the 0-1 knapsack problem in up to 77.8% instances. Then Complementary Strategy Theorem is rigorously proven for applying mixed strategy at the population level. The theorem asserts that given two meta-heuristic algorithms where one uses pure strategy 1 and another uses pure strategy 2, the condition of pure strategy 2 being complementary to pure strategy 1 is sufficient and necessary if there exists a mixed strategy meta-heuristics derived from these two pure strategies and its expected number of generations to find an optimal solution is no more than that of using pure strategy 1 for any initial population, and less than that of using pure strategy 1 for some initial population.

Pure Strategy or Mixed Strategy?

Mixed strategy EAs aim to integrate several mutation operators into a single algorithm. However few theoretical analysis has been made to answer the question whether and when the performance of mixed strategy EAs is better than that of pure strategy EAs. In theory, the performance of EAs can be measured by asymptotic convergence rate and asymptotic hitting time. In this paper, it is proven that given a mixed strategy (1+1) EAs consisting of several mutation operators, its performance (asymptotic convergence rate and asymptotic hitting time)is not worse than that of the worst pure strategy (1+1) EA using one mutation operator; if these mutation operators are mutually complementary, then it is possible to design a mixed strategy (1+1) EA whose performance is better than that of any pure strategy (1+1) EA using one mutation operator.

A Novel Genetic Algorithm using Helper Objectives for the 0-1 Knapsack Problem

The 0-1 knapsack problem is a well-known combinatorial optimisation problem. Approximation algorithms have been designed for solving it and they return provably good solutions within polynomial time. On the other hand, genetic algorithms are well suited for solving the knapsack problem and they find reasonably good solutions quickly. A naturally arising question is whether genetic algorithms are able to find solutions as good as approximation algorithms do. This paper presents a novel multi-objective optimisation genetic algorithm for solving the 0-1 knapsack problem. Experiment results show that the new algorithm outperforms its rivals, the greedy algorithm, mixed strategy genetic algorithm, and greedy algorithm + mixed strategy genetic algorithm.

A Unified Markov Chain Approach to Analysing Randomised Search Heuristics

The convergence, convergence rate and expected hitting time play fundamental roles in the analysis of randomised search heuristics. This paper presents a unified Markov chain approach to studying them. Using the approach, the sufficient and necessary conditions of convergence in distribution are established. Then the average convergence rate is introduced to randomised search heuristics and its lower and upper bounds are derived. Finally, novel average drift analysis and backward drift analysis are proposed for bounding the expected hitting time. A computational study is also conducted to investigate the convergence, convergence rate and expected hitting time. The theoretical study belongs to a prior and general study while the computational study belongs to a posterior and case study.