Wanli Ouyan
Efficient Joint-Dimensional Search with Solution Space Regularization for Real-Time Semantic Segmentation
Aug 10, 2022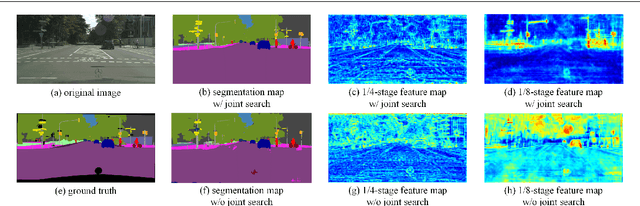
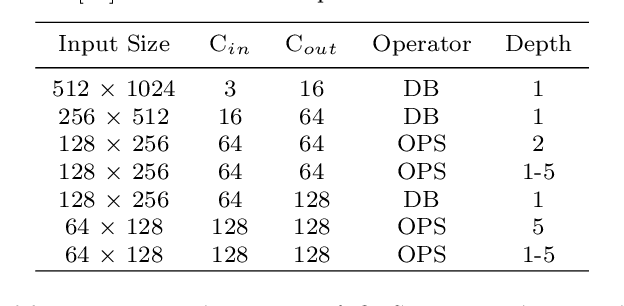
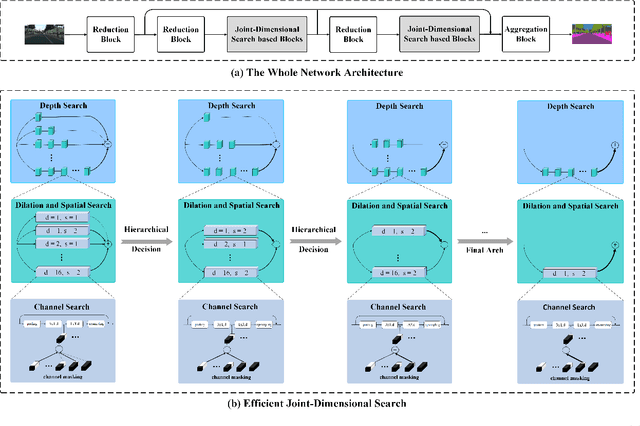
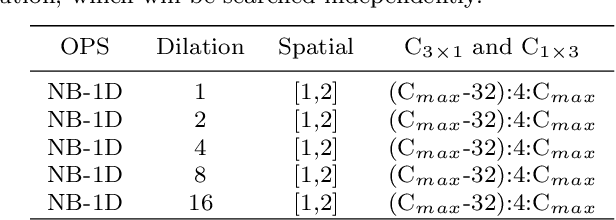
Abstract:Semantic segmentation is a popular research topic in computer vision, and many efforts have been made on it with impressive results. In this paper, we intend to search an optimal network structure that can run in real-time for this problem. Towards this goal, we jointly search the depth, channel, dilation rate and feature spatial resolution, which results in a search space consisting of about 2.78*10^324 possible choices. To handle such a large search space, we leverage differential architecture search methods. However, the architecture parameters searched using existing differential methods need to be discretized, which causes the discretization gap between the architecture parameters found by the differential methods and their discretized version as the final solution for the architecture search. Hence, we relieve the problem of discretization gap from the innovative perspective of solution space regularization. Specifically, a novel Solution Space Regularization (SSR) loss is first proposed to effectively encourage the supernet to converge to its discrete one. Then, a new Hierarchical and Progressive Solution Space Shrinking method is presented to further achieve high efficiency of searching. In addition, we theoretically show that the optimization of SSR loss is equivalent to the L_0-norm regularization, which accounts for the improved search-evaluation gap. Comprehensive experiments show that the proposed search scheme can efficiently find an optimal network structure that yields an extremely fast speed (175 FPS) of segmentation with a small model size (1 M) while maintaining comparable accuracy.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge