Bayesian Federated Learning Via Expectation Maximization and Turbo Deep Approximate Message Passing

Federated learning (FL) is a machine learning paradigm where the clients possess decentralized training data and the central server handles aggregation and scheduling. Typically, FL algorithms involve clients training their local models using stochastic gradient descent (SGD), which carries drawbacks such as slow convergence and being prone to getting stuck in suboptimal solutions. In this work, we propose a message passing based Bayesian federated learning (BFL) framework to avoid these drawbacks.Specifically, we formulate the problem of deep neural network (DNN) learning and compression and as a sparse Bayesian inference problem, in which group sparse prior is employed to achieve structured model compression. Then, we propose an efficient BFL algorithm called EMTDAMP, where expectation maximization (EM) and turbo deep approximate message passing (TDAMP) are combined to achieve distributed learning and compression. The central server aggregates local posterior distributions to update global posterior distributions and update hyperparameters based on EM to accelerate convergence. The clients perform TDAMP to achieve efficient approximate message passing over DNN with joint prior distribution. We detail the application of EMTDAMP to Boston housing price prediction and handwriting recognition, and present extensive numerical results to demonstrate the advantages of EMTDAMP.

GQFedWAvg: Optimization-Based Quantized Federated Learning in General Edge Computing Systems

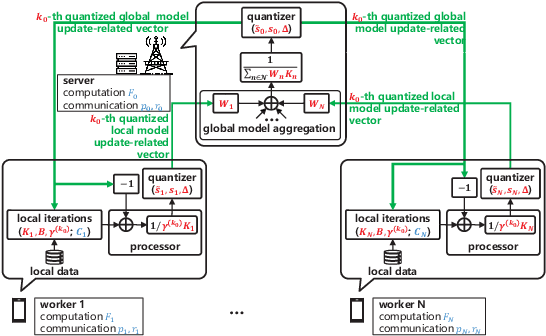
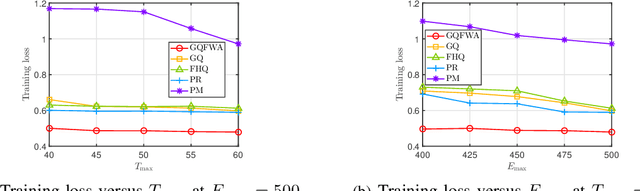
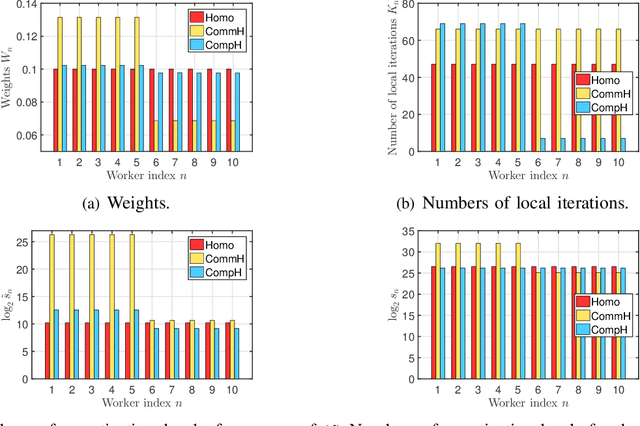
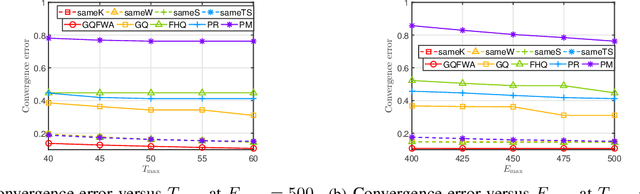
The optimal implementation of federated learning (FL) in practical edge computing systems has been an outstanding problem. In this paper, we propose an optimization-based quantized FL algorithm, which can appropriately fit a general edge computing system with uniform or nonuniform computing and communication resources at the workers. Specifically, we first present a new random quantization scheme and analyze its properties. Then, we propose a general quantized FL algorithm, namely GQFedWAvg. Specifically, GQFedWAvg applies the proposed quantization scheme to quantize wisely chosen model update-related vectors and adopts a generalized mini-batch stochastic gradient descent (SGD) method with the weighted average local model updates in global model aggregation. Besides, GQFedWAvg has several adjustable algorithm parameters to flexibly adapt to the computing and communication resources at the server and workers. We also analyze the convergence of GQFedWAvg. Next, we optimize the algorithm parameters of GQFedWAvg to minimize the convergence error under the time and energy constraints. We successfully tackle the challenging non-convex problem using general inner approximation (GIA) and multiple delicate tricks. Finally, we interpret GQFedWAvg's function principle and show its considerable gains over existing FL algorithms using numerical results.

Riemannian Low-Rank Model Compression for Federated Learning with Over-the-Air Aggregation

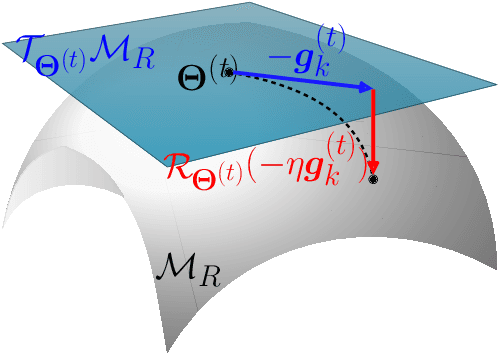
Low-rank model compression is a widely used technique for reducing the computational load when training machine learning models. However, existing methods often rely on relaxing the low-rank constraint of the model weights using a regularized nuclear norm penalty, which requires an appropriate hyperparameter that can be difficult to determine in practice. Furthermore, existing compression techniques are not directly applicable to efficient over-the-air (OTA) aggregation in federated learning (FL) systems for distributed Internet-of-Things (IoT) scenarios. In this paper, we propose a novel manifold optimization formulation for low-rank model compression in FL that does not relax the low-rank constraint. Our optimization is conducted directly over the low-rank manifold, guaranteeing that the model is exactly low-rank. We also introduce a consensus penalty in the optimization formulation to support OTA aggregation. Based on our optimization formulation, we propose an alternating Riemannian optimization algorithm with a precoder that enables efficient OTA aggregation of low-rank local models without sacrificing training performance. Additionally, we provide convergence analysis in terms of key system parameters and conduct extensive experiments with real-world datasets to demonstrate the effectiveness of our proposed Riemannian low-rank model compression scheme compared to various state-of-the-art baselines.

Joint Activity Detection and Channel Estimation in Massive Machine-Type Communications with Low-Resolution ADC

In massive machine-type communications, data transmission is usually considered sporadic, and thus inherently has a sparse structure. This paper focuses on the joint activity detection (AD) and channel estimation (CE) problems in massive-connected communication systems with low-resolution analog-to-digital converters. To further exploit the sparse structure in transmission, we propose a maximum posterior probability (MAP) estimation problem based on both sporadic activity and sparse channels for joint AD and CE. Moreover, a majorization-minimization-based method is proposed for solving the MAP problem. Finally, various numerical experiments verify that the proposed scheme outperforms state-of-the-art methods.

An Optimization Framework for Federated Edge Learning

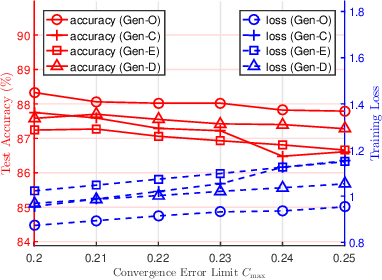
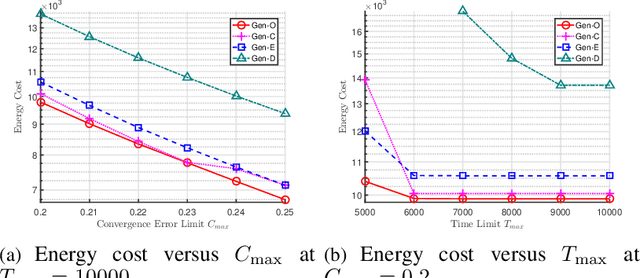
The optimal design of federated learning (FL) algorithms for solving general machine learning (ML) problems in practical edge computing systems with quantized message passing remains an open problem. This paper considers an edge computing system where the server and workers have possibly different computing and communication capabilities and employ quantization before transmitting messages. To explore the full potential of FL in such an edge computing system, we first present a general FL algorithm, namely GenQSGD, parameterized by the numbers of global and local iterations, mini-batch size, and step size sequence. Then, we analyze its convergence for an arbitrary step size sequence and specify the convergence results under three commonly adopted step size rules, namely the constant, exponential, and diminishing step size rules. Next, we optimize the algorithm parameters to minimize the energy cost under the time constraint and convergence error constraint, with the focus on the overall implementing process of FL. Specifically, for any given step size sequence under each considered step size rule, we optimize the numbers of global and local iterations and mini-batch size to optimally implement FL for applications with preset step size sequences. We also optimize the step size sequence along with these algorithm parameters to explore the full potential of FL. The resulting optimization problems are challenging non-convex problems with non-differentiable constraint functions. We propose iterative algorithms to obtain KKT points using general inner approximation (GIA) and tricks for solving complementary geometric programming (CGP). Finally, we numerically demonstrate the remarkable gains of GenQSGD with optimized algorithm parameters over existing FL algorithms and reveal the significance of optimally designing general FL algorithms.

Optimization-Based GenQSGD for Federated Edge Learning

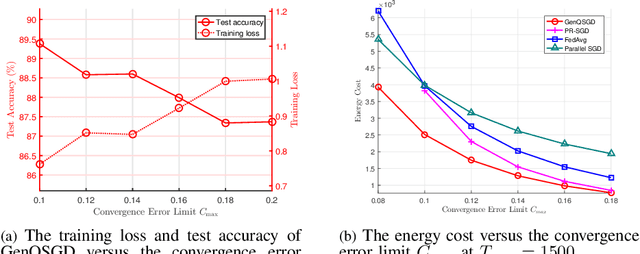
Optimal algorithm design for federated learning (FL) remains an open problem. This paper explores the full potential of FL in practical edge computing systems where workers may have different computation and communication capabilities, and quantized intermediate model updates are sent between the server and workers. First, we present a general quantized parallel mini-batch stochastic gradient descent (SGD) algorithm for FL, namely GenQSGD, which is parameterized by the number of global iterations, the numbers of local iterations at all workers, and the mini-batch size. We also analyze its convergence error for any choice of the algorithm parameters. Then, we optimize the algorithm parameters to minimize the energy cost under the time constraint and convergence error constraint. The optimization problem is a challenging non-convex problem with non-differentiable constraint functions. We propose an iterative algorithm to obtain a KKT point using advanced optimization techniques. Numerical results demonstrate the significant gains of GenQSGD over existing FL algorithms and reveal the importance of optimally designing FL algorithms.

Efficient Sparse Coding using Hierarchical Riemannian Pursuit

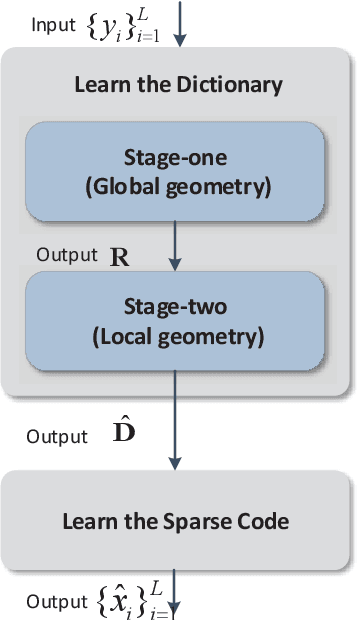
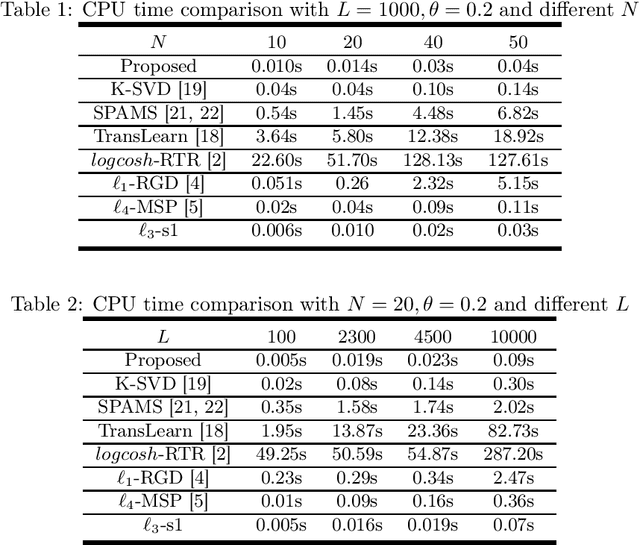
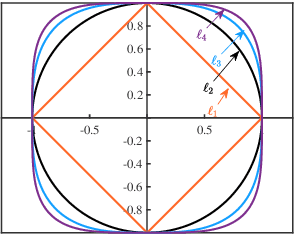
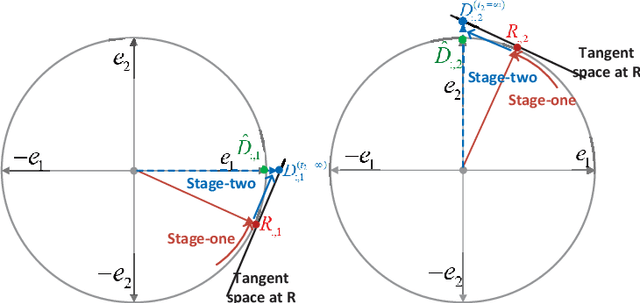
Sparse coding is a class of unsupervised methods for learning a sparse representation of the input data in the form of a linear combination of a dictionary and a sparse code. This learning framework has led to state-of-the-art results in various image and video processing tasks. However, classical methods learn the dictionary and the sparse code based on alternative optimizations, usually without theoretical guarantees for either optimality or convergence due to non-convexity of the problem. Recent works on sparse coding with a complete dictionary provide strong theoretical guarantees thanks to the development of the non-convex optimization. However, initial non-convex approaches learn the dictionary in the sparse coding problem sequentially in an atom-by-atom manner, which leads to a long execution time. More recent works seek to directly learn the entire dictionary at once, which substantially reduces the execution time. However, the associated recovery performance is degraded with a finite number of data samples. In this paper, we propose an efficient sparse coding scheme with a two-stage optimization. The proposed scheme leverages the global and local Riemannian geometry of the two-stage optimization problem and facilitates fast implementation for superb dictionary recovery performance by a finite number of samples without atom-by-atom calculation. We further prove that, with high probability, the proposed scheme can exactly recover any atom in the target dictionary with a finite number of samples if it is adopted to recover one atom of the dictionary. An application on wireless sensor data compression is also proposed. Experiments on both synthetic and real-world data verify the efficiency and effectiveness of the proposed scheme.

Online Orthogonal Dictionary Learning Based on Frank-Wolfe Method

Dictionary learning is a widely used unsupervised learning method in signal processing and machine learning. Most existing works of dictionary learning are in an offline manner. There are mainly two offline ways for dictionary learning. One is to do an alternative optimization of both the dictionary and the sparse code; the other way is to optimize the dictionary by restricting it over the orthogonal group. The latter one is called orthogonal dictionary learning which has a lower complexity implementation, hence, it is more favorable for lowcost devices. However, existing schemes on orthogonal dictionary learning only work with batch data and can not be implemented online, which is not applicable for real-time applications. This paper proposes a novel online orthogonal dictionary scheme to dynamically learn the dictionary from streaming data without storing the historical data. The proposed scheme includes a novel problem formulation and an efficient online algorithm design with convergence analysis. In the problem formulation, we relax the orthogonal constraint to enable an efficient online algorithm. In the algorithm design, we propose a new Frank-Wolfe-based online algorithm with a convergence rate of O(ln t/t^(1/4)). The convergence rate in terms of key system parameters is also derived. Experiments with synthetic data and real-world sensor readings demonstrate the effectiveness and efficiency of the proposed online orthogonal dictionary learning scheme.

Complete Dictionary Learning via $\ell_p$-norm Maximization

Dictionary learning is a classic representation learning method that has been widely applied in signal processing and data analytics. In this paper, we investigate a family of $\ell_p$-norm ($p>2,p \in \mathbb{N}$) maximization approaches for the complete dictionary learning problem from theoretical and algorithmic aspects. Specifically, we prove that the global maximizers of these formulations are very close to the true dictionary with high probability, even when Gaussian noise is present. Based on the generalized power method (GPM), an efficient algorithm is then developed for the $\ell_p$-based formulations. We further show the efficacy of the developed algorithm: for the population GPM algorithm over the sphere constraint, it first quickly enters the neighborhood of a global maximizer, and then converges linearly in this region. Extensive experiments will demonstrate that the $\ell_p$-based approaches enjoy a higher computational efficiency and better robustness than conventional approaches and $p=3$ performs the best.