Sequential Offloading for Distributed DNN Computation in Multiuser MEC Systems

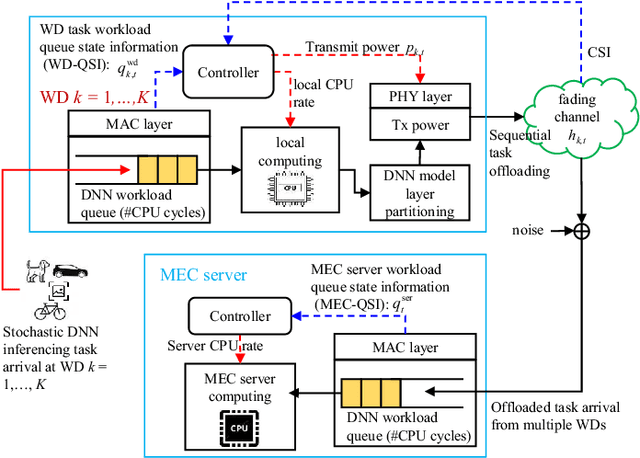
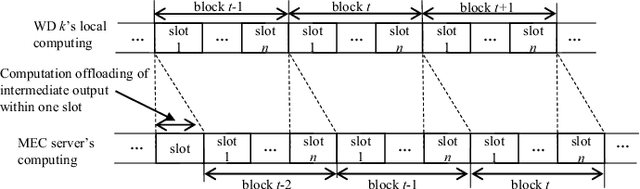
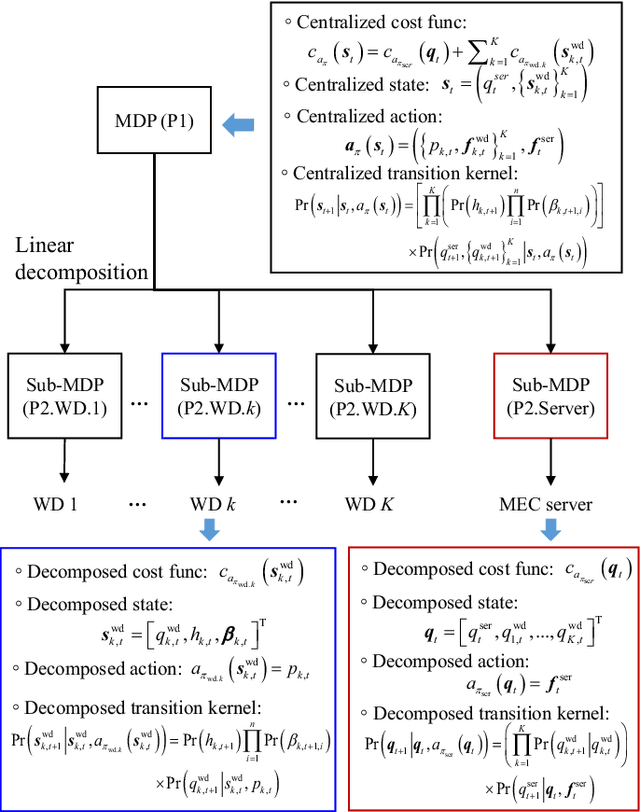
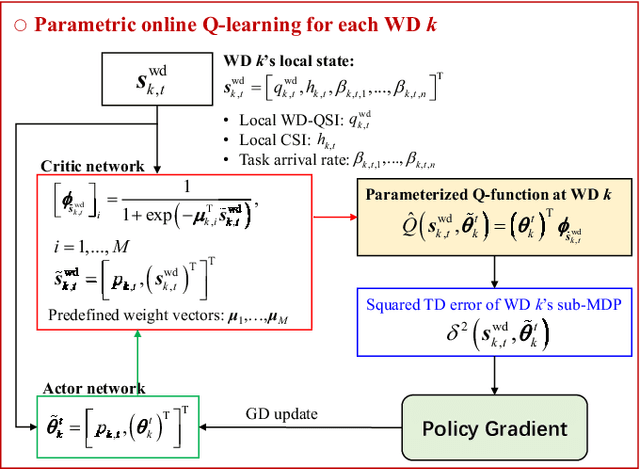
This paper studies a sequential task offloading problem for a multiuser mobile edge computing (MEC) system. We consider a dynamic optimization approach, which embraces wireless channel fluctuations and random deep neural network (DNN) task arrivals over an infinite horizon. Specifically, we introduce a local CPU workload queue (WD-QSI) and an MEC server workload queue (MEC-QSI) to model the dynamic workload of DNN tasks at each WD and the MEC server, respectively. The transmit power and the partitioning of the local DNN task at each WD are dynamically determined based on the instantaneous channel conditions (to capture the transmission opportunities) and the instantaneous WD-QSI and MEC-QSI (to capture the dynamic urgency of the tasks) to minimize the average latency of the DNN tasks. The joint optimization can be formulated as an ergodic Markov decision process (MDP), in which the optimality condition is characterized by a centralized Bellman equation. However, the brute force solution of the MDP is not viable due to the curse of dimensionality as well as the requirement for knowledge of the global state information. To overcome these issues, we first decompose the MDP into multiple lower dimensional sub-MDPs, each of which can be associated with a WD or the MEC server. Next, we further develop a parametric online Q-learning algorithm, so that each sub-MDP is solved locally at its associated WD or the MEC server. The proposed solution is completely decentralized in the sense that the transmit power for sequential offloading and the DNN task partitioning can be determined based on the local channel state information (CSI) and the local WD-QSI at the WD only. Additionally, no prior knowledge of the distribution of the DNN task arrivals or the channel statistics will be needed for the MEC server.

Efficient Sparse Coding using Hierarchical Riemannian Pursuit

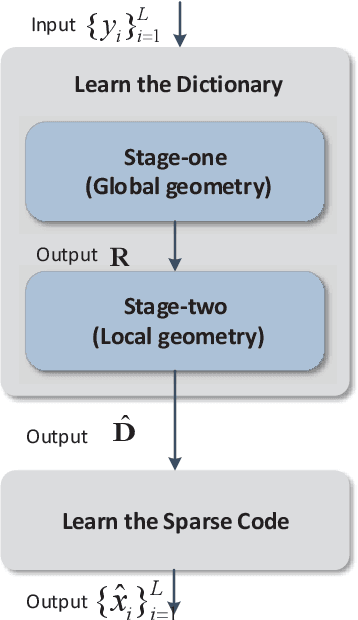
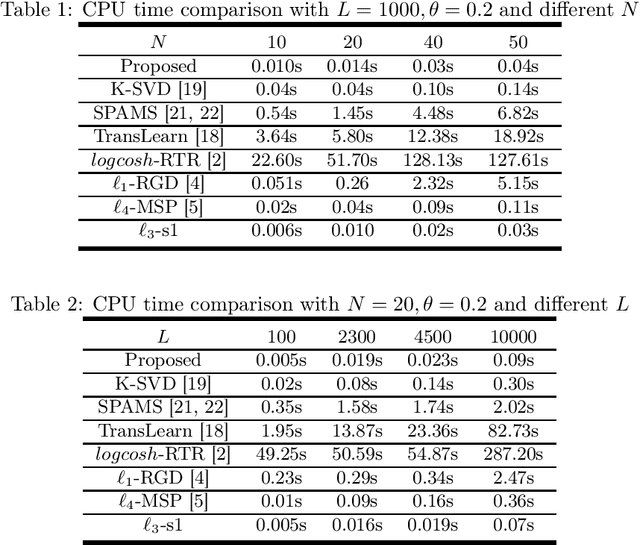
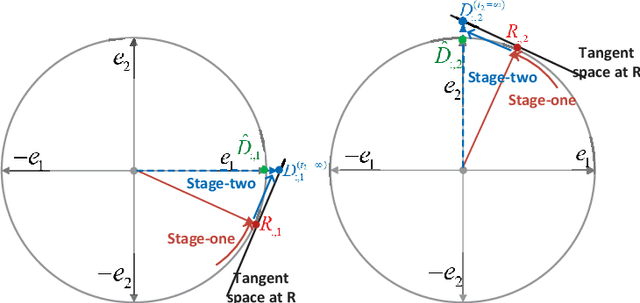
Sparse coding is a class of unsupervised methods for learning a sparse representation of the input data in the form of a linear combination of a dictionary and a sparse code. This learning framework has led to state-of-the-art results in various image and video processing tasks. However, classical methods learn the dictionary and the sparse code based on alternative optimizations, usually without theoretical guarantees for either optimality or convergence due to non-convexity of the problem. Recent works on sparse coding with a complete dictionary provide strong theoretical guarantees thanks to the development of the non-convex optimization. However, initial non-convex approaches learn the dictionary in the sparse coding problem sequentially in an atom-by-atom manner, which leads to a long execution time. More recent works seek to directly learn the entire dictionary at once, which substantially reduces the execution time. However, the associated recovery performance is degraded with a finite number of data samples. In this paper, we propose an efficient sparse coding scheme with a two-stage optimization. The proposed scheme leverages the global and local Riemannian geometry of the two-stage optimization problem and facilitates fast implementation for superb dictionary recovery performance by a finite number of samples without atom-by-atom calculation. We further prove that, with high probability, the proposed scheme can exactly recover any atom in the target dictionary with a finite number of samples if it is adopted to recover one atom of the dictionary. An application on wireless sensor data compression is also proposed. Experiments on both synthetic and real-world data verify the efficiency and effectiveness of the proposed scheme.