Yangchen Li
GQFedWAvg: Optimization-Based Quantized Federated Learning in General Edge Computing Systems
Jun 13, 2023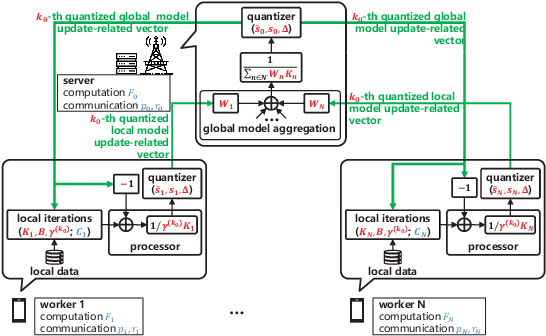
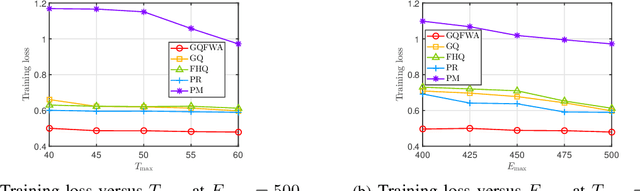
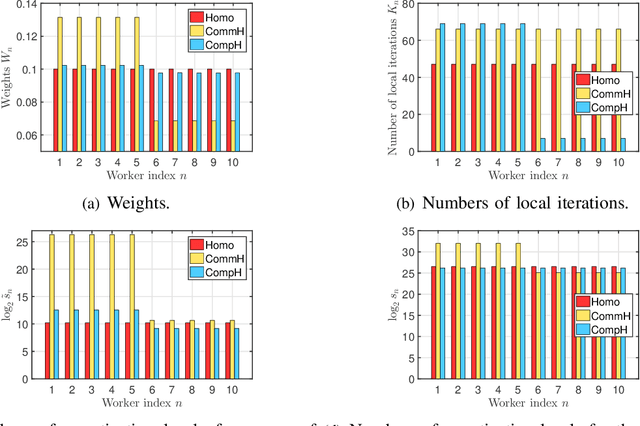
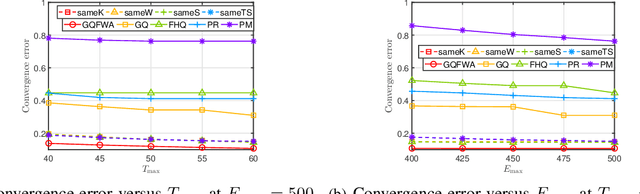
Abstract:The optimal implementation of federated learning (FL) in practical edge computing systems has been an outstanding problem. In this paper, we propose an optimization-based quantized FL algorithm, which can appropriately fit a general edge computing system with uniform or nonuniform computing and communication resources at the workers. Specifically, we first present a new random quantization scheme and analyze its properties. Then, we propose a general quantized FL algorithm, namely GQFedWAvg. Specifically, GQFedWAvg applies the proposed quantization scheme to quantize wisely chosen model update-related vectors and adopts a generalized mini-batch stochastic gradient descent (SGD) method with the weighted average local model updates in global model aggregation. Besides, GQFedWAvg has several adjustable algorithm parameters to flexibly adapt to the computing and communication resources at the server and workers. We also analyze the convergence of GQFedWAvg. Next, we optimize the algorithm parameters of GQFedWAvg to minimize the convergence error under the time and energy constraints. We successfully tackle the challenging non-convex problem using general inner approximation (GIA) and multiple delicate tricks. Finally, we interpret GQFedWAvg's function principle and show its considerable gains over existing FL algorithms using numerical results.
An Optimization Framework for Federated Edge Learning
Nov 26, 2021

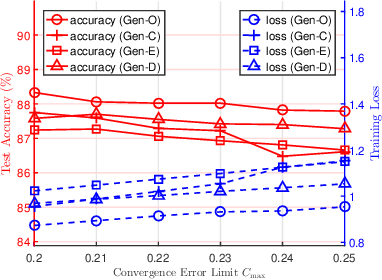
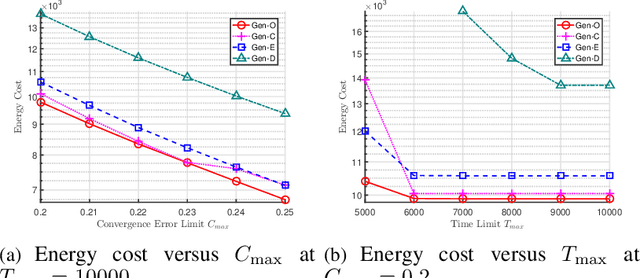
Abstract:The optimal design of federated learning (FL) algorithms for solving general machine learning (ML) problems in practical edge computing systems with quantized message passing remains an open problem. This paper considers an edge computing system where the server and workers have possibly different computing and communication capabilities and employ quantization before transmitting messages. To explore the full potential of FL in such an edge computing system, we first present a general FL algorithm, namely GenQSGD, parameterized by the numbers of global and local iterations, mini-batch size, and step size sequence. Then, we analyze its convergence for an arbitrary step size sequence and specify the convergence results under three commonly adopted step size rules, namely the constant, exponential, and diminishing step size rules. Next, we optimize the algorithm parameters to minimize the energy cost under the time constraint and convergence error constraint, with the focus on the overall implementing process of FL. Specifically, for any given step size sequence under each considered step size rule, we optimize the numbers of global and local iterations and mini-batch size to optimally implement FL for applications with preset step size sequences. We also optimize the step size sequence along with these algorithm parameters to explore the full potential of FL. The resulting optimization problems are challenging non-convex problems with non-differentiable constraint functions. We propose iterative algorithms to obtain KKT points using general inner approximation (GIA) and tricks for solving complementary geometric programming (CGP). Finally, we numerically demonstrate the remarkable gains of GenQSGD with optimized algorithm parameters over existing FL algorithms and reveal the significance of optimally designing general FL algorithms.
Optimization-Based GenQSGD for Federated Edge Learning
Nov 26, 2021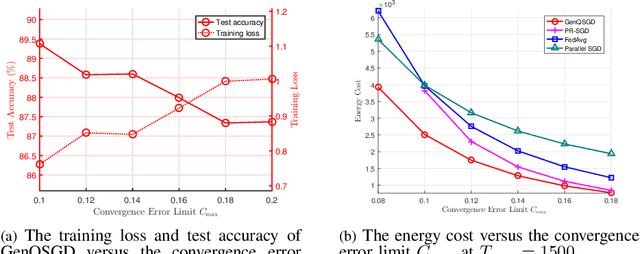
Abstract:Optimal algorithm design for federated learning (FL) remains an open problem. This paper explores the full potential of FL in practical edge computing systems where workers may have different computation and communication capabilities, and quantized intermediate model updates are sent between the server and workers. First, we present a general quantized parallel mini-batch stochastic gradient descent (SGD) algorithm for FL, namely GenQSGD, which is parameterized by the number of global iterations, the numbers of local iterations at all workers, and the mini-batch size. We also analyze its convergence error for any choice of the algorithm parameters. Then, we optimize the algorithm parameters to minimize the energy cost under the time constraint and convergence error constraint. The optimization problem is a challenging non-convex problem with non-differentiable constraint functions. We propose an iterative algorithm to obtain a KKT point using advanced optimization techniques. Numerical results demonstrate the significant gains of GenQSGD over existing FL algorithms and reveal the importance of optimally designing FL algorithms.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge