Deep Reinforcement Learning for Dexterous Manipulation with Concept Networks

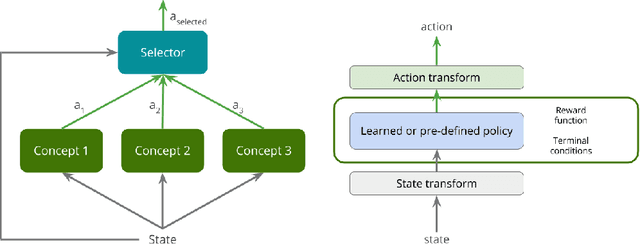
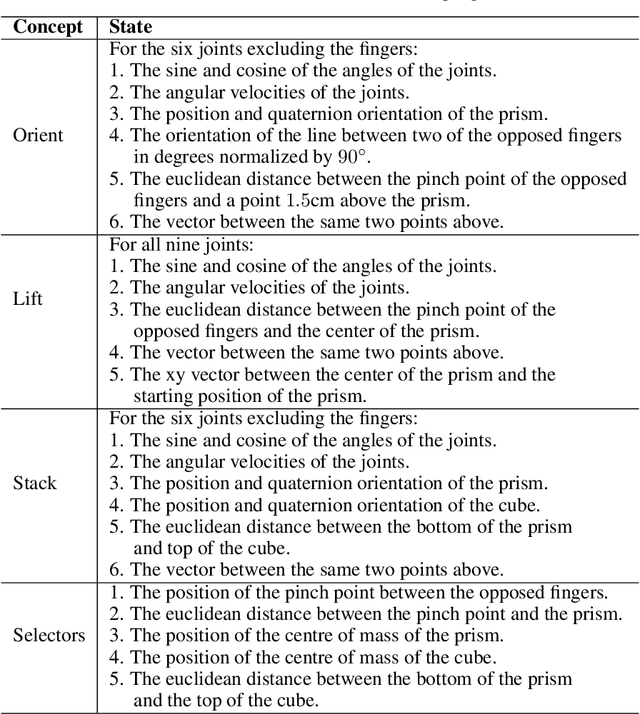
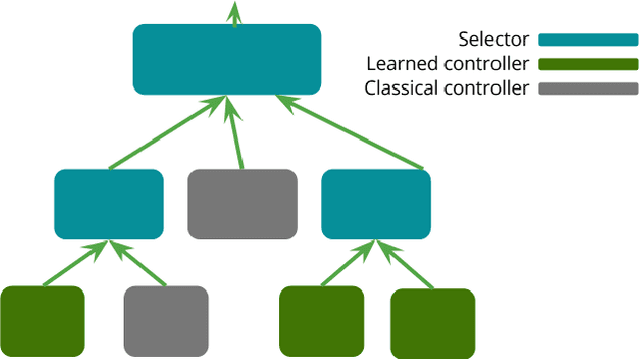
Deep reinforcement learning yields great results for a large array of problems, but models are generally retrained anew for each new problem to be solved. Prior learning and knowledge are difficult to incorporate when training new models, requiring increasingly longer training as problems become more complex. This is especially problematic for problems with sparse rewards. We provide a solution to these problems by introducing Concept Network Reinforcement Learning (CNRL), a framework which allows us to decompose problems using a multi-level hierarchy. Concepts in a concept network are reusable, and flexible enough to encapsulate feature extractors, skills, or other concept networks. With this hierarchical learning approach, deep reinforcement learning can be used to solve complex tasks in a modular way, through problem decomposition. We demonstrate the strength of CNRL by training a model to grasp a rectangular prism and precisely stack it on top of a cube using a gripper on a Kinova JACO arm, simulated in MuJoCo. Our experiments show that our use of hierarchy results in a 45x reduction in environment interactions compared to the state-of-the-art on this task.

Combining Independent Modules in Lexical Multiple-Choice Problems

Existing statistical approaches to natural language problems are very coarse approximations to the true complexity of language processing. As such, no single technique will be best for all problem instances. Many researchers are examining ensemble methods that combine the output of multiple modules to create more accurate solutions. This paper examines three merging rules for combining probability distributions: the familiar mixture rule, the logarithmic rule, and a novel product rule. These rules were applied with state-of-the-art results to two problems used to assess human mastery of lexical semantics -- synonym questions and analogy questions. All three merging rules result in ensembles that are more accurate than any of their component modules. The differences among the three rules are not statistically significant, but it is suggestive that the popular mixture rule is not the best rule for either of the two problems.

Combining Independent Modules to Solve Multiple-choice Synonym and Analogy Problems

Existing statistical approaches to natural language problems are very coarse approximations to the true complexity of language processing. As such, no single technique will be best for all problem instances. Many researchers are examining ensemble methods that combine the output of successful, separately developed modules to create more accurate solutions. This paper examines three merging rules for combining probability distributions: the well known mixture rule, the logarithmic rule, and a novel product rule. These rules were applied with state-of-the-art results to two problems commonly used to assess human mastery of lexical semantics -- synonym questions and analogy questions. All three merging rules result in ensembles that are more accurate than any of their component modules. The differences among the three rules are not statistically significant, but it is suggestive that the popular mixture rule is not the best rule for either of the two problems.