Deep Reinforcement Learning for Dexterous Manipulation with Concept Networks

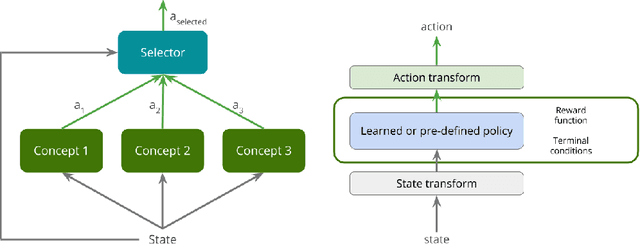
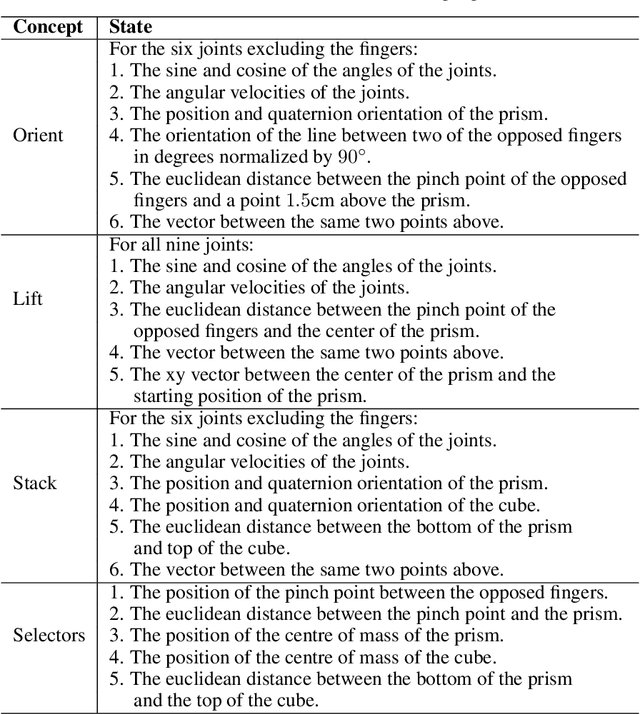
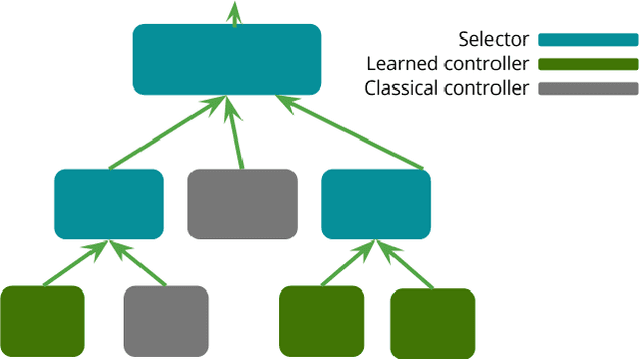
Deep reinforcement learning yields great results for a large array of problems, but models are generally retrained anew for each new problem to be solved. Prior learning and knowledge are difficult to incorporate when training new models, requiring increasingly longer training as problems become more complex. This is especially problematic for problems with sparse rewards. We provide a solution to these problems by introducing Concept Network Reinforcement Learning (CNRL), a framework which allows us to decompose problems using a multi-level hierarchy. Concepts in a concept network are reusable, and flexible enough to encapsulate feature extractors, skills, or other concept networks. With this hierarchical learning approach, deep reinforcement learning can be used to solve complex tasks in a modular way, through problem decomposition. We demonstrate the strength of CNRL by training a model to grasp a rectangular prism and precisely stack it on top of a cube using a gripper on a Kinova JACO arm, simulated in MuJoCo. Our experiments show that our use of hierarchy results in a 45x reduction in environment interactions compared to the state-of-the-art on this task.

Manifold unwrapping using density ridges

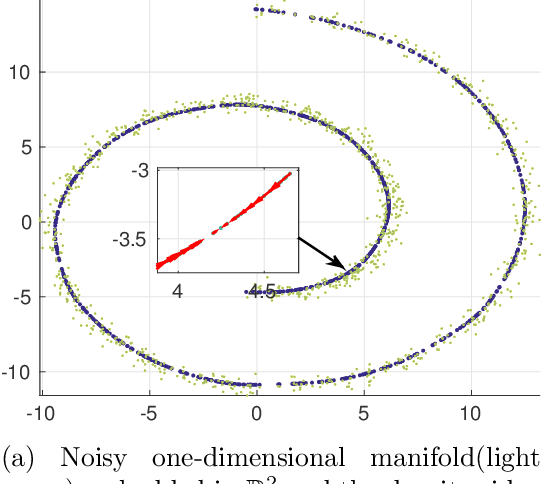
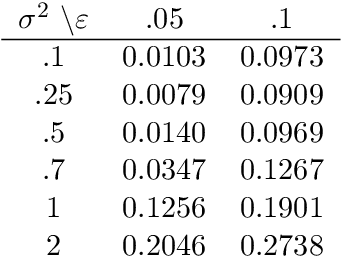
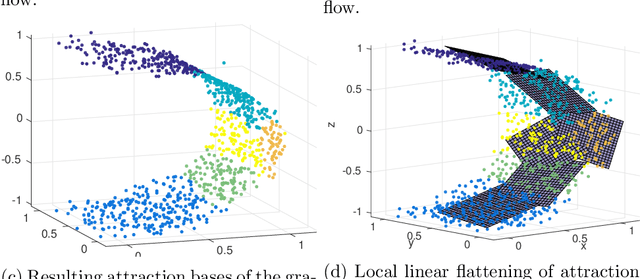
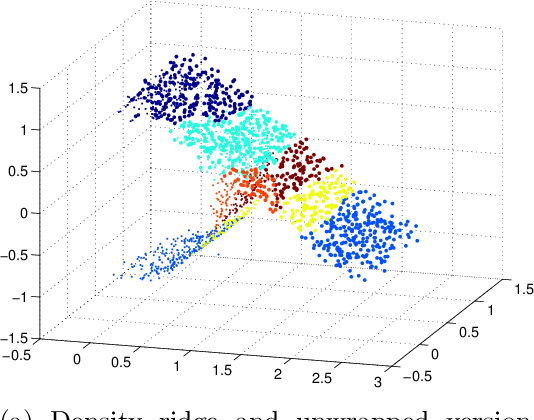
Research on manifold learning within a density ridge estimation framework has shown great potential in recent work for both estimation and de-noising of manifolds, building on the intuitive and well-defined notion of principal curves and surfaces. However, the problem of unwrapping or unfolding manifolds has received relatively little attention within the density ridge approach, despite being an integral part of manifold learning in general. This paper proposes two novel algorithms for unwrapping manifolds based on estimated principal curves and surfaces for one- and multi-dimensional manifolds respectively. The methods of unwrapping are founded in the realization that both principal curves and principal surfaces will have inherent local maxima of the probability density function. Following this observation, coordinate systems that follow the shape of the manifold can be computed by following the integral curves of the gradient flow of a kernel density estimate on the manifold. Furthermore, since integral curves of the gradient flow of a kernel density estimate is inherently local, we propose to stitch together local coordinate systems using parallel transport along the manifold. We provide numerical experiments on both real and synthetic data that illustrates clear and intuitive unwrapping results comparable to state-of-the-art manifold learning algorithms.