Simpler is better: spectral regularization and up-sampling techniques for variational autoencoders

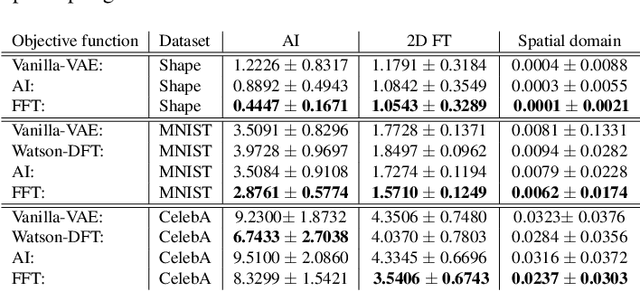
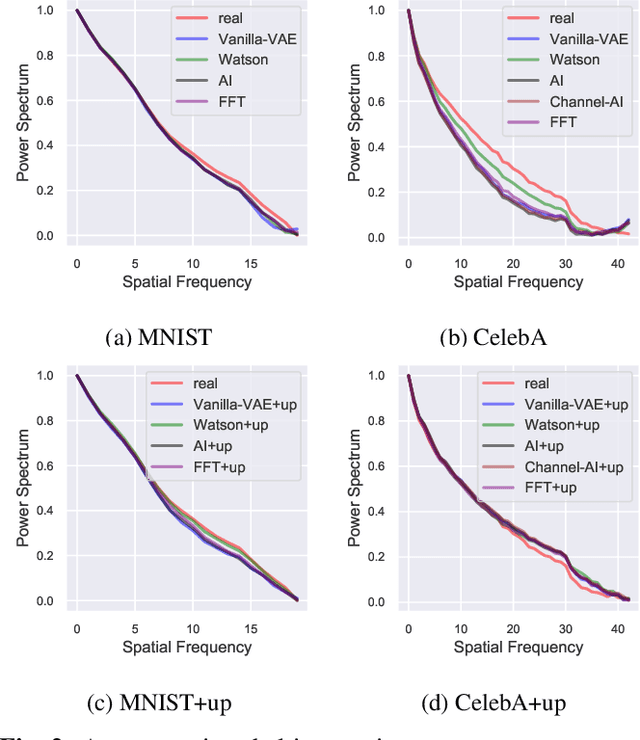
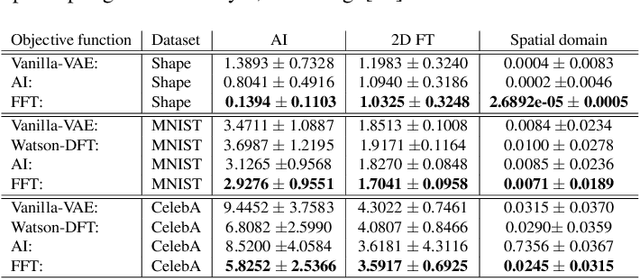
Full characterization of the spectral behavior of generative models based on neural networks remains an open issue. Recent research has focused heavily on generative adversarial networks and the high-frequency discrepancies between real and generated images. The current solution to avoid this is to either replace transposed convolutions with bilinear up-sampling or add a spectral regularization term in the generator. It is well known that Variational Autoencoders (VAEs) also suffer from these issues. In this work, we propose a simple 2D Fourier transform-based spectral regularization loss for the VAE and show that it can achieve results equal to, or better than, the current state-of-the-art in frequency-aware losses for generative models. In addition, we experiment with altering the up-sampling procedure in the generator network and investigate how it influences the spectral performance of the model. We include experiments on synthetic and real data sets to demonstrate our results.

Manifold unwrapping using density ridges

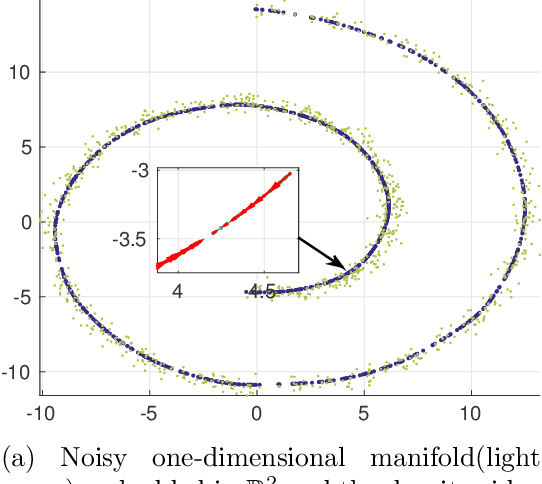
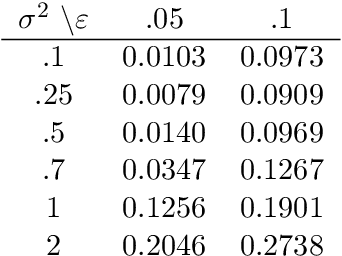
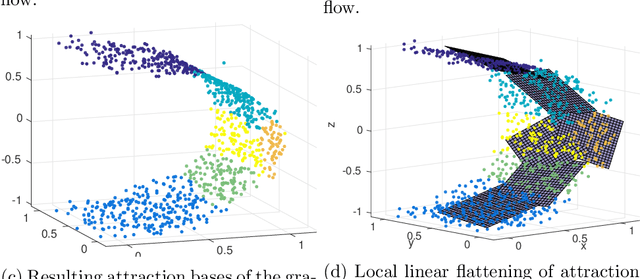
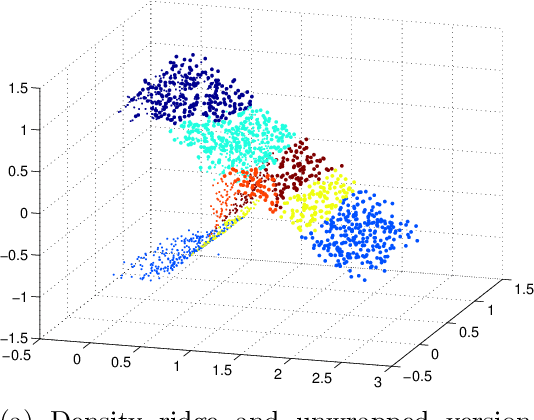
Research on manifold learning within a density ridge estimation framework has shown great potential in recent work for both estimation and de-noising of manifolds, building on the intuitive and well-defined notion of principal curves and surfaces. However, the problem of unwrapping or unfolding manifolds has received relatively little attention within the density ridge approach, despite being an integral part of manifold learning in general. This paper proposes two novel algorithms for unwrapping manifolds based on estimated principal curves and surfaces for one- and multi-dimensional manifolds respectively. The methods of unwrapping are founded in the realization that both principal curves and principal surfaces will have inherent local maxima of the probability density function. Following this observation, coordinate systems that follow the shape of the manifold can be computed by following the integral curves of the gradient flow of a kernel density estimate on the manifold. Furthermore, since integral curves of the gradient flow of a kernel density estimate is inherently local, we propose to stitch together local coordinate systems using parallel transport along the manifold. We provide numerical experiments on both real and synthetic data that illustrates clear and intuitive unwrapping results comparable to state-of-the-art manifold learning algorithms.