Vicenc Rubies-Royo
Expert Selection in High-Dimensional Markov Decision Processes
Oct 26, 2020
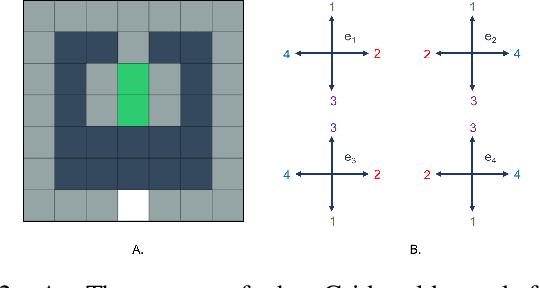
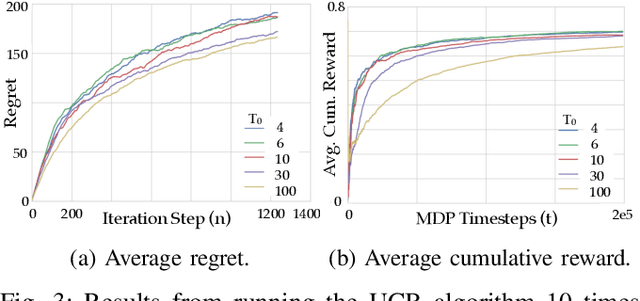
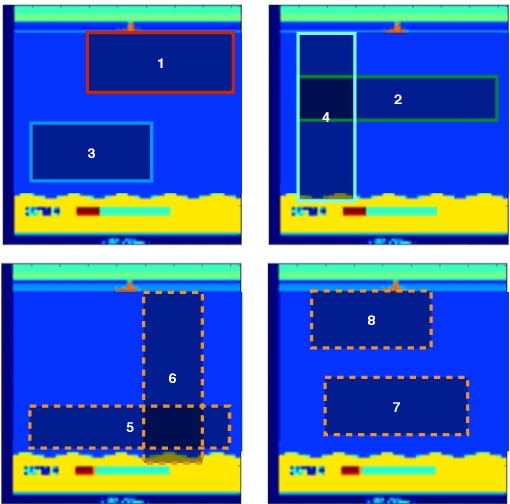
Abstract:In this work we present a multi-armed bandit framework for online expert selection in Markov decision processes and demonstrate its use in high-dimensional settings. Our method takes a set of candidate expert policies and switches between them to rapidly identify the best performing expert using a variant of the classical upper confidence bound algorithm, thus ensuring low regret in the overall performance of the system. This is useful in applications where several expert policies may be available, and one needs to be selected at run-time for the underlying environment.
An Iterative Quadratic Method for General-Sum Differential Games with Feedback Linearizable Dynamics
Oct 01, 2019



Abstract:Iterative linear-quadratic (ILQ) methods are widely used in the nonlinear optimal control community. Recent work has applied similar methodology in the setting of multi-player general-sum differential games. Here, ILQ methods are capable of finding local Nash equilibria in interactive motion planning problems in real-time. As in most iterative procedures, however, this approach can be sensitive to initial conditions and hyperparameter choices, which can result in poor computational performance or even unsafe trajectories. In this paper, we focus our attention on a broad class of dynamical systems which are feedback linearizable, and exploit this structure to improve both algorithmic reliability and runtime. We showcase our new algorithm in three distinct traffic scenarios, and observe that in practice our method converges significantly more often and more quickly than was possible without exploiting the feedback linearizable structure.
Fast Neural Network Verification via Shadow Prices
Mar 08, 2019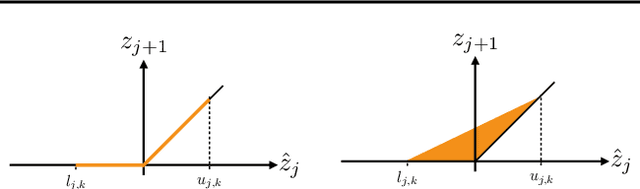
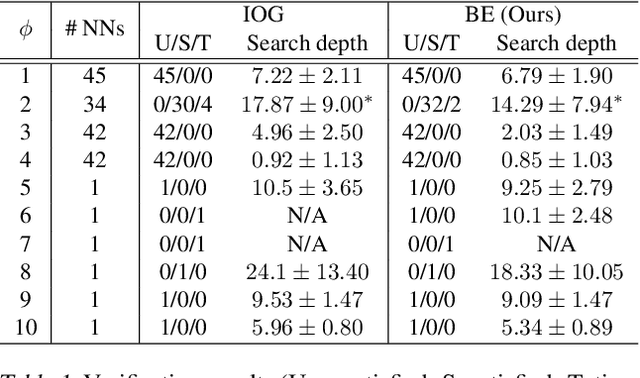

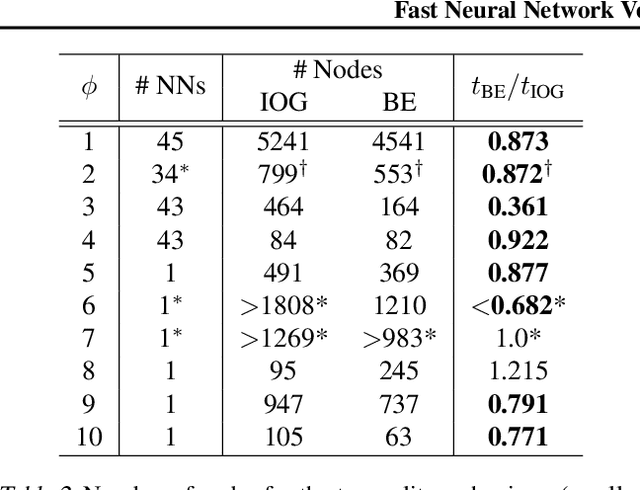
Abstract:To use neural networks in safety-critical settings it is paramount to provide assurances on their runtime operation. Recent work on ReLU networks has sought to verify whether inputs belonging to a bounded box can ever yield some undesirable output. Input-splitting procedures, a particular type of verification mechanism, do so by recursively partitioning the input set into smaller sets. The efficiency of these methods is largely determined by the number of splits the box must undergo before the property can be verified. In this work, we propose a new technique based on shadow prices that fully exploits the information of the problem yielding a more efficient generation of splits than the state-of-the-art. Results on the Airborne Collision Avoidance System (ACAS) benchmark verification tasks show a considerable reduction in the partitions generated which substantially reduces computation times. These results open the door to improved verification methods for a wide variety of machine learning applications including vision and control.
Classification-based Approximate Reachability with Guarantees Applied to Safe Trajectory Tracking
Mar 08, 2018


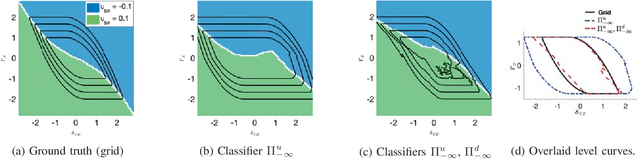
Abstract:Hamilton-Jacobi (HJ) reachability analysis has been developed over the past decades into a widely-applicable tool for determining goal satisfaction and safety verification in nonlinear systems. While HJ reachability can be formulated very generally, computational complexity can be a serious impediment for many systems of practical interest. Much prior work has been devoted to computing approximate solutions to large reachability problems, yet many of these methods apply to only restricted problem classes, do not generate controllers, and/or are extremely conservative. In this paper, we present a novel approach to approximate HJ reachability in which computing an optimal controller is viewed as a sequential classification problem. Even though we employ neural networks for this classification task, our method still provides safety guarantees in many cases. We demonstrate the utility of our approach in the context of safe trajectory following with specific application to quadrotor navigation. Offline computation and online evaluation confirm that our method preserves safety.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge