Large Scale Graph Learning from Smooth Signals

Graphs are a prevalent tool in data science, as they model the inherent structure of the data. They have been used successfully in unsupervised and semi-supervised learning. Typically they are constructed either by connecting nearest samples, or by learning them from data, solving an optimization problem. While graph learning does achieve a better quality, it also comes with a higher computational cost. In particular, the current state-of-the-art model cost is $\mathcal{O}(n^2)$ for $n$ samples. In this paper, we show how to scale it, obtaining an approximation with leading cost of $\mathcal{O}(n\log(n))$, with quality that approaches the exact graph learning model. Our algorithm uses known approximate nearest neighbor techniques to reduce the number of variables, and automatically selects the correct parameters of the model, requiring a single intuitive input: the desired edge density.

UNLocBoX: A MATLAB convex optimization toolbox for proximal-splitting methods

Convex optimization is an essential tool for machine learning, as many of its problems can be formulated as minimization problems of specific objective functions. While there is a large variety of algorithms available to solve convex problems, we can argue that it becomes more and more important to focus on efficient, scalable methods that can deal with big data. When the objective function can be written as a sum of "simple" terms, proximal splitting methods are a good choice. UNLocBoX is a MATLAB library that implements many of these methods, designed to solve convex optimization problems of the form $\min_{x \in \mathbb{R}^N} \sum_{n=1}^K f_n(x).$ It contains the most recent solvers such as FISTA, Douglas-Rachford, SDMM as well a primal dual techniques such as Chambolle-Pock and forward-backward-forward. It also includes an extensive list of common proximal operators that can be combined, allowing for a quick implementation of a large variety of convex problems.

Fast Robust PCA on Graphs

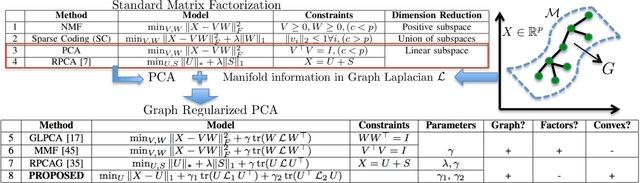
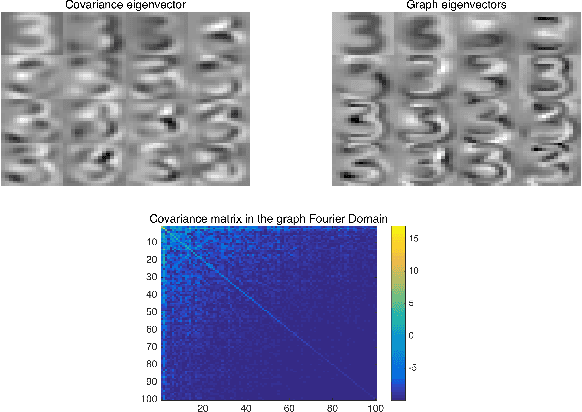
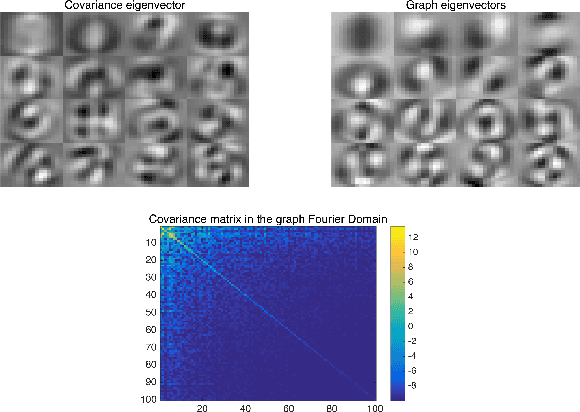
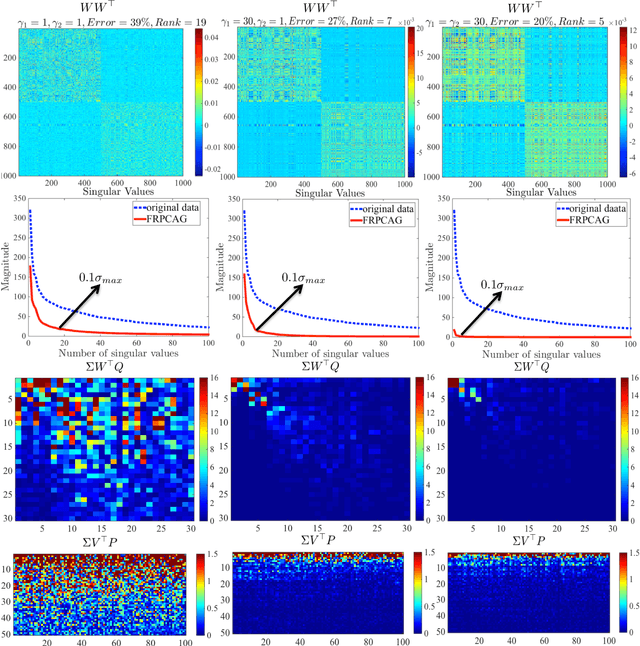
Mining useful clusters from high dimensional data has received significant attention of the computer vision and pattern recognition community in the recent years. Linear and non-linear dimensionality reduction has played an important role to overcome the curse of dimensionality. However, often such methods are accompanied with three different problems: high computational complexity (usually associated with the nuclear norm minimization), non-convexity (for matrix factorization methods) and susceptibility to gross corruptions in the data. In this paper we propose a principal component analysis (PCA) based solution that overcomes these three issues and approximates a low-rank recovery method for high dimensional datasets. We target the low-rank recovery by enforcing two types of graph smoothness assumptions, one on the data samples and the other on the features by designing a convex optimization problem. The resulting algorithm is fast, efficient and scalable for huge datasets with O(nlog(n)) computational complexity in the number of data samples. It is also robust to gross corruptions in the dataset as well as to the model parameters. Clustering experiments on 7 benchmark datasets with different types of corruptions and background separation experiments on 3 video datasets show that our proposed model outperforms 10 state-of-the-art dimensionality reduction models. Our theoretical analysis proves that the proposed model is able to recover approximate low-rank representations with a bounded error for clusterable data.

Song Recommendation with Non-Negative Matrix Factorization and Graph Total Variation

This work formulates a novel song recommender system as a matrix completion problem that benefits from collaborative filtering through Non-negative Matrix Factorization (NMF) and content-based filtering via total variation (TV) on graphs. The graphs encode both playlist proximity information and song similarity, using a rich combination of audio, meta-data and social features. As we demonstrate, our hybrid recommendation system is very versatile and incorporates several well-known methods while outperforming them. Particularly, we show on real-world data that our model overcomes w.r.t. two evaluation metrics the recommendation of models solely based on low-rank information, graph-based information or a combination of both.

How to learn a graph from smooth signals

We propose a framework that learns the graph structure underlying a set of smooth signals. Given $X\in\mathbb{R}^{m\times n}$ whose rows reside on the vertices of an unknown graph, we learn the edge weights $w\in\mathbb{R}_+^{m(m-1)/2}$ under the smoothness assumption that $\text{tr}{X^\top LX}$ is small. We show that the problem is a weighted $\ell$-1 minimization that leads to naturally sparse solutions. We point out how known graph learning or construction techniques fall within our framework and propose a new model that performs better than the state of the art in many settings. We present efficient, scalable primal-dual based algorithms for both our model and the previous state of the art, and evaluate their performance on artificial and real data.

Robust Principal Component Analysis on Graphs

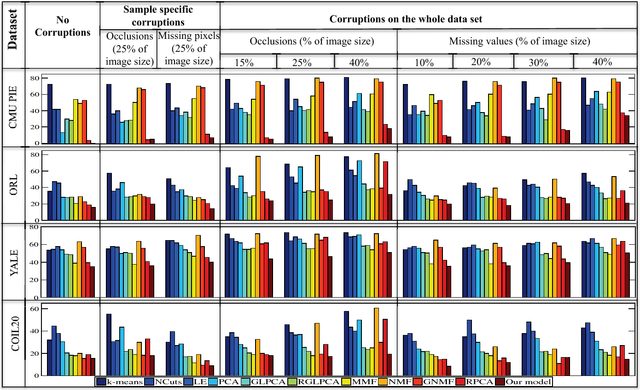
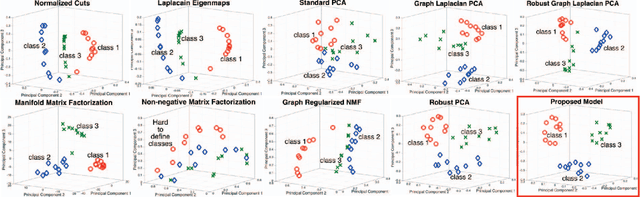
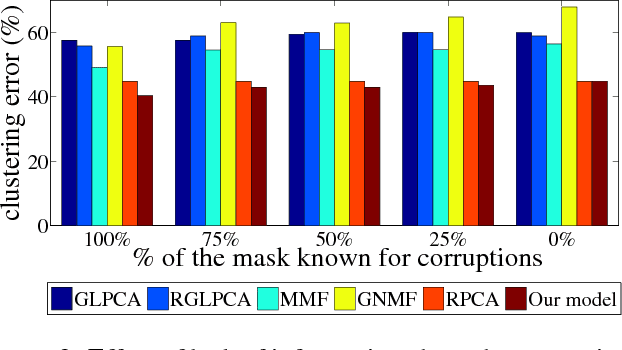
Principal Component Analysis (PCA) is the most widely used tool for linear dimensionality reduction and clustering. Still it is highly sensitive to outliers and does not scale well with respect to the number of data samples. Robust PCA solves the first issue with a sparse penalty term. The second issue can be handled with the matrix factorization model, which is however non-convex. Besides, PCA based clustering can also be enhanced by using a graph of data similarity. In this article, we introduce a new model called "Robust PCA on Graphs" which incorporates spectral graph regularization into the Robust PCA framework. Our proposed model benefits from 1) the robustness of principal components to occlusions and missing values, 2) enhanced low-rank recovery, 3) improved clustering property due to the graph smoothness assumption on the low-rank matrix, and 4) convexity of the resulting optimization problem. Extensive experiments on 8 benchmark, 3 video and 2 artificial datasets with corruptions clearly reveal that our model outperforms 10 other state-of-the-art models in its clustering and low-rank recovery tasks.

Matrix Completion on Graphs

The problem of finding the missing values of a matrix given a few of its entries, called matrix completion, has gathered a lot of attention in the recent years. Although the problem under the standard low rank assumption is NP-hard, Cand\`es and Recht showed that it can be exactly relaxed if the number of observed entries is sufficiently large. In this work, we introduce a novel matrix completion model that makes use of proximity information about rows and columns by assuming they form communities. This assumption makes sense in several real-world problems like in recommender systems, where there are communities of people sharing preferences, while products form clusters that receive similar ratings. Our main goal is thus to find a low-rank solution that is structured by the proximities of rows and columns encoded by graphs. We borrow ideas from manifold learning to constrain our solution to be smooth on these graphs, in order to implicitly force row and column proximities. Our matrix recovery model is formulated as a convex non-smooth optimization problem, for which a well-posed iterative scheme is provided. We study and evaluate the proposed matrix completion on synthetic and real data, showing that the proposed structured low-rank recovery model outperforms the standard matrix completion model in many situations.