Vanessa Didelez
Constraint-based causal discovery with tiered background knowledge and latent variables in single or overlapping datasets
Mar 27, 2025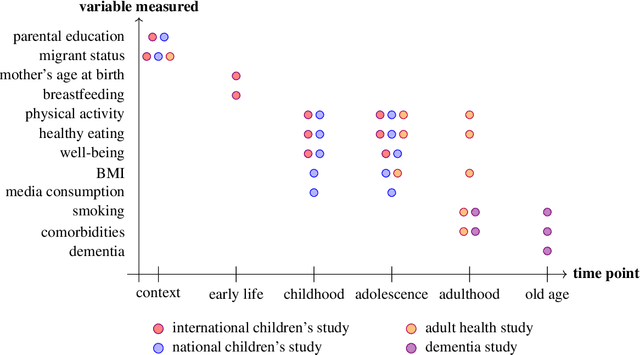



Abstract:In this paper we consider the use of tiered background knowledge within constraint based causal discovery. Our focus is on settings relaxing causal sufficiency, i.e. allowing for latent variables which may arise because relevant information could not be measured at all, or not jointly, as in the case of multiple overlapping datasets. We first present novel insights into the properties of the 'tiered FCI' (tFCI) algorithm. Building on this, we introduce a new extension of the IOD (integrating overlapping datasets) algorithm incorporating tiered background knowledge, the 'tiered IOD' (tIOD) algorithm. We show that under full usage of the tiered background knowledge tFCI and tIOD are sound, while simple versions of the tIOD and tFCI are sound and complete. We further show that the tIOD algorithm can often be expected to be considerably more efficient and informative than the IOD algorithm even beyond the obvious restriction of the Markov equivalence classes. We provide a formal result on the conditions for this gain in efficiency and informativeness. Our results are accompanied by a series of examples illustrating the exact role and usefulness of tiered background knowledge.
Robot Pouring: Identifying Causes of Spillage and Selecting Alternative Action Parameters Using Probabilistic Actual Causation
Feb 13, 2025Abstract:In everyday life, we perform tasks (e.g., cooking or cleaning) that involve a large variety of objects and goals. When confronted with an unexpected or unwanted outcome, we take corrective actions and try again until achieving the desired result. The reasoning performed to identify a cause of the observed outcome and to select an appropriate corrective action is a crucial aspect of human reasoning for successful task execution. Central to this reasoning is the assumption that a factor is responsible for producing the observed outcome. In this paper, we investigate the use of probabilistic actual causation to determine whether a factor is the cause of an observed undesired outcome. Furthermore, we show how the actual causation probabilities can be used to find alternative actions to change the outcome. We apply the probabilistic actual causation analysis to a robot pouring task. When spillage occurs, the analysis indicates whether a task parameter is the cause and how it should be changed to avoid spillage. The analysis requires a causal graph of the task and the corresponding conditional probability distributions. To fulfill these requirements, we perform a complete causal modeling procedure (i.e., task analysis, definition of variables, determination of the causal graph structure, and estimation of conditional probability distributions) using data from a realistic simulation of the robot pouring task, covering a large combinatorial space of task parameters. Based on the results, we discuss the implications of the variables' representation and how the alternative actions suggested by the actual causation analysis would compare to the alternative solutions proposed by a human observer. The practical use of the analysis of probabilistic actual causation to select alternative action parameters is demonstrated.
Improving Finite Sample Performance of Causal Discovery by Exploiting Temporal Structure
Jun 27, 2024Abstract:Methods of causal discovery aim to identify causal structures in a data driven way. Existing algorithms are known to be unstable and sensitive to statistical errors, and are therefore rarely used with biomedical or epidemiological data. We present an algorithm that efficiently exploits temporal structure, so-called tiered background knowledge, for estimating causal structures. Tiered background knowledge is readily available from, e.g., cohort or registry data. When used efficiently it renders the algorithm more robust to statistical errors and ultimately increases accuracy in finite samples. We describe the algorithm and illustrate how it proceeds. Moreover, we offer formal proofs as well as examples of desirable properties of the algorithm, which we demonstrate empirically in an extensive simulation study. To illustrate its usefulness in practice, we apply the algorithm to data from a children's cohort study investigating the interplay of diet, physical activity and other lifestyle factors for health outcomes.
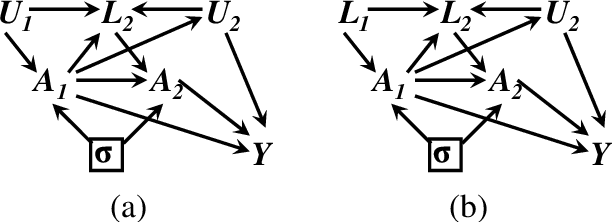
Do we become wiser with time? On causal equivalence with tiered background knowledge
Jun 02, 2023



Abstract:Equivalence classes of DAGs (represented by CPDAGs) may be too large to provide useful causal information. Here, we address incorporating tiered background knowledge yielding restricted equivalence classes represented by 'tiered MPDAGs'. Tiered knowledge leads to considerable gains in informativeness and computational efficiency: We show that construction of tiered MPDAGs only requires application of Meek's 1st rule, and that tiered MPDAGs (unlike general MPDAGs) are chain graphs with chordal components. This entails simplifications e.g. of determining valid adjustment sets for causal effect estimation. Further, we characterise when one tiered ordering is more informative than another, providing insights into useful aspects of background knowledge.
Multiple imputation and test-wise deletion for causal discovery with incomplete cohort data
Aug 30, 2021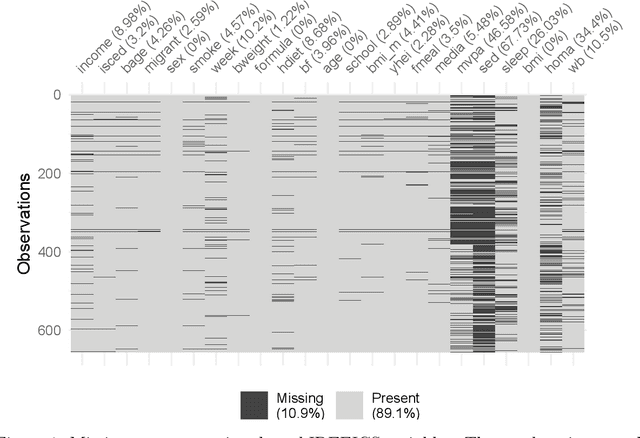

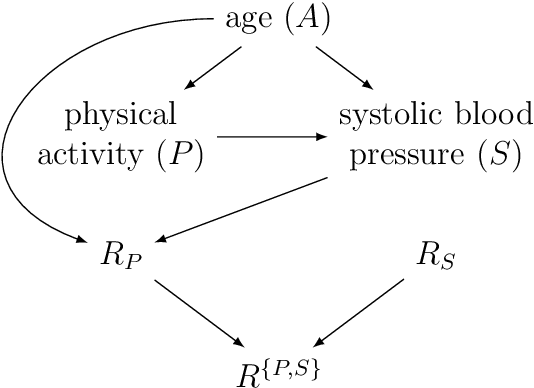
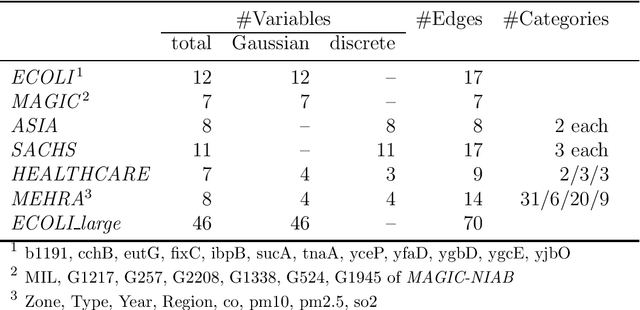
Abstract:Causal discovery algorithms estimate causal graphs from observational data. This can provide a valuable complement to analyses focussing on the causal relation between individual treatment-outcome pairs. Constraint-based causal discovery algorithms rely on conditional independence testing when building the graph. Until recently, these algorithms have been unable to handle missing values. In this paper, we investigate two alternative solutions: Test-wise deletion and multiple imputation. We establish necessary and sufficient conditions for the recoverability of causal structures under test-wise deletion, and argue that multiple imputation is more challenging in the context of causal discovery than for estimation. We conduct an extensive comparison by simulating from benchmark causal graphs: As one might expect, we find that test-wise deletion and multiple imputation both clearly outperform list-wise deletion and single imputation. Crucially, our results further suggest that multiple imputation is especially useful in settings with a small number of either Gaussian or discrete variables, but when the dataset contains a mix of both neither method is uniformly best. The methods we compare include random forest imputation and a hybrid procedure combining test-wise deletion and multiple imputation. An application to data from the IDEFICS cohort study on diet- and lifestyle-related diseases in European children serves as an illustrating example.
Asymmetric separation for local independence graphs
Jun 27, 2012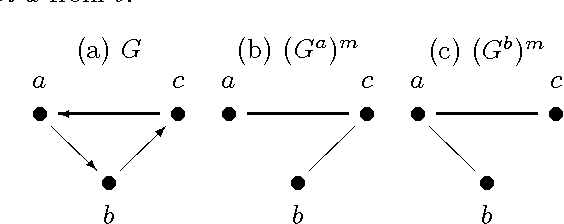
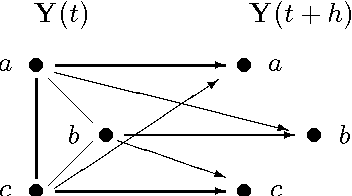
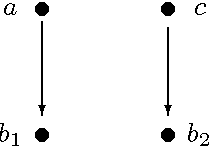
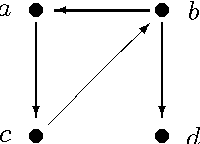
Abstract:Directed possibly cyclic graphs have been proposed by Didelez (2000) and Nodelmann et al. (2002) in order to represent the dynamic dependencies among stochastic processes. These dependencies are based on a generalization of Granger-causality to continuous time, first developed by Schweder (1970) for Markov processes, who called them local dependencies. They deserve special attention as they are asymmetric unlike stochastic (in)dependence. In this paper we focus on their graphical representation and develop a suitable, i.e. asymmetric notion of separation, called delta-separation. The properties of this graph separation as well as of local independence are investigated in detail within a framework of asymmetric (semi)graphoids allowing a deeper insight into what information can be read off these graphs.
Causal Reasoning in Graphical Time Series Models
Jun 20, 2012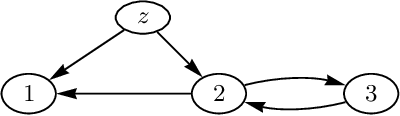


Abstract:We propose a definition of causality for time series in terms of the effect of an intervention in one component of a multivariate time series on another component at some later point in time. Conditions for identifiability, comparable to the back-door and front-door criteria, are presented and can also be verified graphically. Computation of the causal effect is derived and illustrated for the linear case.
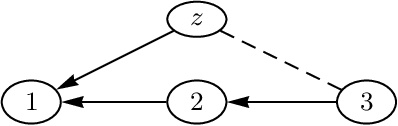
Identifying Optimal Sequential Decisions
Jun 13, 2012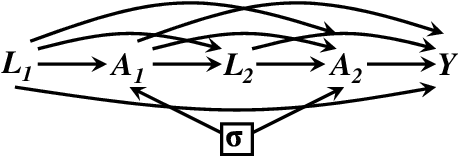
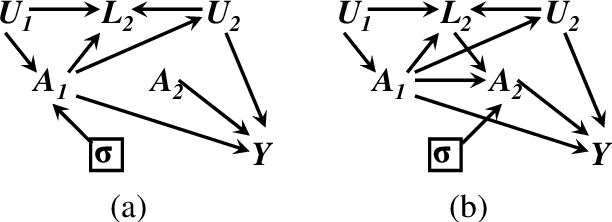
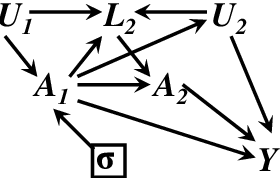
Abstract:We consider conditions that allow us to find an optimal strategy for sequential decisions from a given data situation. For the case where all interventions are unconditional (atomic), identifiability has been discussed by Pearl & Robins (1995). We argue here that an optimal strategy must be conditional, i.e. take the information available at each decision point into account. We show that the identification of an optimal sequential decision strategy is more restrictive, in the sense that conditional interventions might not always be identified when atomic interventions are. We further demonstrate that a simple graphical criterion for the identifiability of an optimal strategy can be given.
Identifying the consequences of dynamic treatment strategies: A decision-theoretic overview
Oct 17, 2010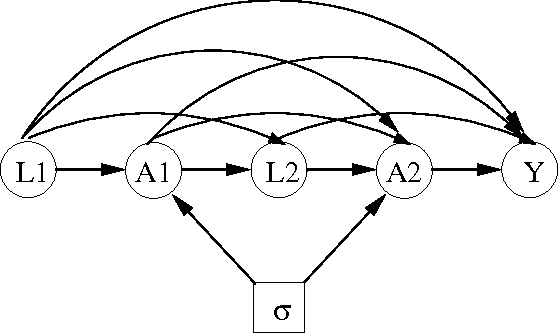
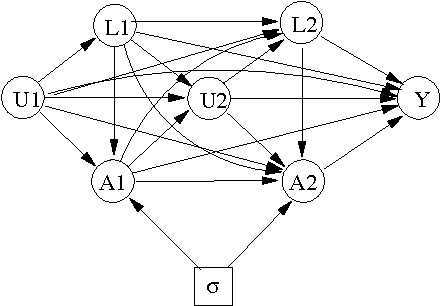
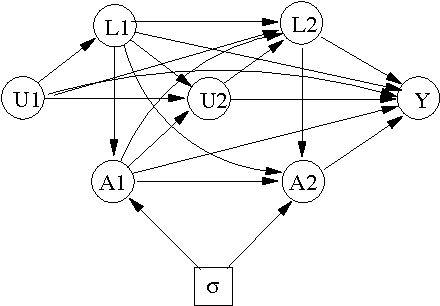
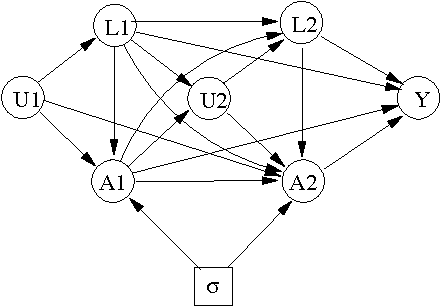
Abstract:We consider the problem of learning about and comparing the consequences of dynamic treatment strategies on the basis of observational data. We formulate this within a probabilistic decision-theoretic framework. Our approach is compared with related work by Robins and others: in particular, we show how Robins's 'G-computation' algorithm arises naturally from this decision-theoretic perspective. Careful attention is paid to the mathematical and substantive conditions required to justify the use of this formula. These conditions revolve around a property we term stability, which relates the probabilistic behaviours of observational and interventional regimes. We show how an assumption of 'sequential randomization' (or 'no unmeasured confounders'), or an alternative assumption of 'sequential irrelevance', can be used to infer stability. Probabilistic influence diagrams are used to simplify manipulations, and their power and limitations are discussed. We compare our approach with alternative formulations based on causal DAGs or potential response models. We aim to show that formulating the problem of assessing dynamic treatment strategies as a problem of decision analysis brings clarity, simplicity and generality.
* 49 pages, 15 figures
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge