Asymmetric separation for local independence graphs
Paper and Code
Jun 27, 2012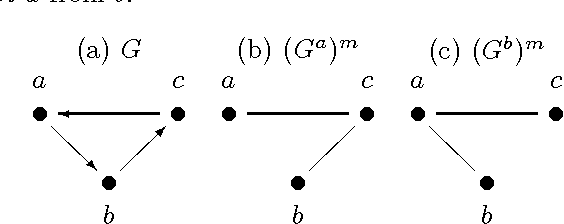
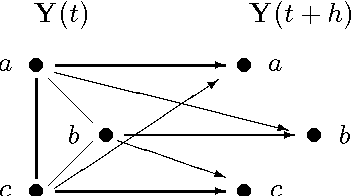
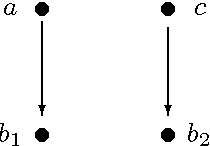
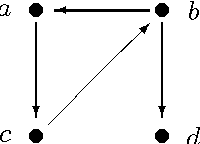
Directed possibly cyclic graphs have been proposed by Didelez (2000) and Nodelmann et al. (2002) in order to represent the dynamic dependencies among stochastic processes. These dependencies are based on a generalization of Granger-causality to continuous time, first developed by Schweder (1970) for Markov processes, who called them local dependencies. They deserve special attention as they are asymmetric unlike stochastic (in)dependence. In this paper we focus on their graphical representation and develop a suitable, i.e. asymmetric notion of separation, called delta-separation. The properties of this graph separation as well as of local independence are investigated in detail within a framework of asymmetric (semi)graphoids allowing a deeper insight into what information can be read off these graphs.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge