On Learnability under General Stochastic Processes

Statistical learning theory under independent and identically distributed (iid) sampling and online learning theory for worst case individual sequences are two of the best developed branches of learning theory. Statistical learning under general non-iid stochastic processes is less mature. We provide two natural notions of learnability of a function class under a general stochastic process. We are able to sandwich the first one between iid and online learnability. We show that the second one is in fact equivalent to online learnability. Our results are sharpest in the binary classification setting but we also show that similar results continue to hold in the regression setting.

Identifying the consequences of dynamic treatment strategies: A decision-theoretic overview

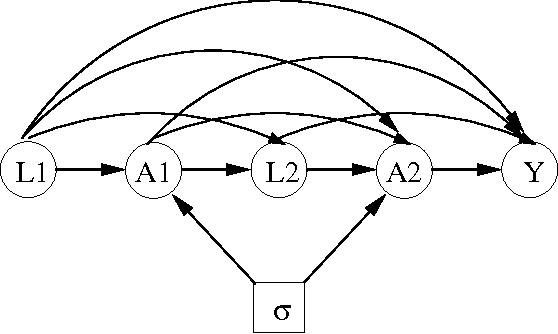
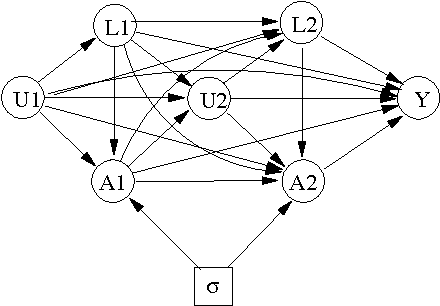
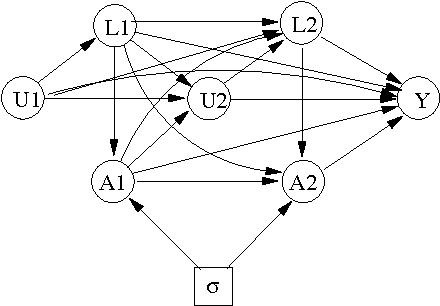
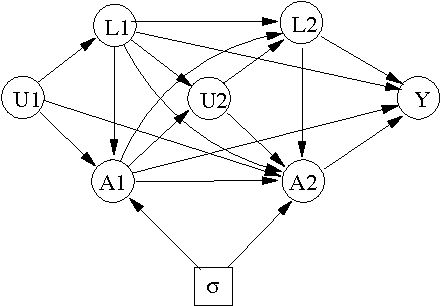
We consider the problem of learning about and comparing the consequences of dynamic treatment strategies on the basis of observational data. We formulate this within a probabilistic decision-theoretic framework. Our approach is compared with related work by Robins and others: in particular, we show how Robins's 'G-computation' algorithm arises naturally from this decision-theoretic perspective. Careful attention is paid to the mathematical and substantive conditions required to justify the use of this formula. These conditions revolve around a property we term stability, which relates the probabilistic behaviours of observational and interventional regimes. We show how an assumption of 'sequential randomization' (or 'no unmeasured confounders'), or an alternative assumption of 'sequential irrelevance', can be used to infer stability. Probabilistic influence diagrams are used to simplify manipulations, and their power and limitations are discussed. We compare our approach with alternative formulations based on causal DAGs or potential response models. We aim to show that formulating the problem of assessing dynamic treatment strategies as a problem of decision analysis brings clarity, simplicity and generality.