Improving Finite Sample Performance of Causal Discovery by Exploiting Temporal Structure

Methods of causal discovery aim to identify causal structures in a data driven way. Existing algorithms are known to be unstable and sensitive to statistical errors, and are therefore rarely used with biomedical or epidemiological data. We present an algorithm that efficiently exploits temporal structure, so-called tiered background knowledge, for estimating causal structures. Tiered background knowledge is readily available from, e.g., cohort or registry data. When used efficiently it renders the algorithm more robust to statistical errors and ultimately increases accuracy in finite samples. We describe the algorithm and illustrate how it proceeds. Moreover, we offer formal proofs as well as examples of desirable properties of the algorithm, which we demonstrate empirically in an extensive simulation study. To illustrate its usefulness in practice, we apply the algorithm to data from a children's cohort study investigating the interplay of diet, physical activity and other lifestyle factors for health outcomes.

Multiple imputation and test-wise deletion for causal discovery with incomplete cohort data

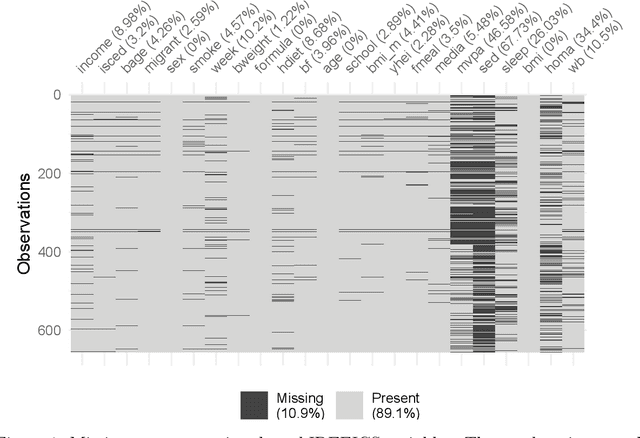
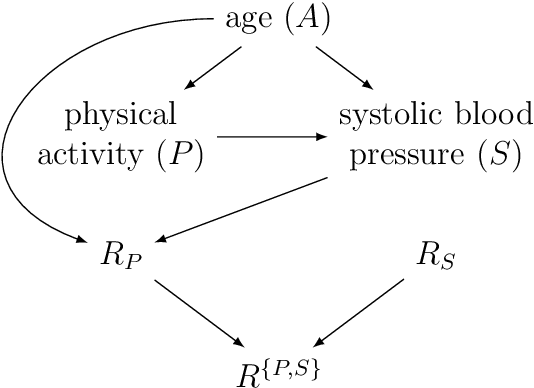
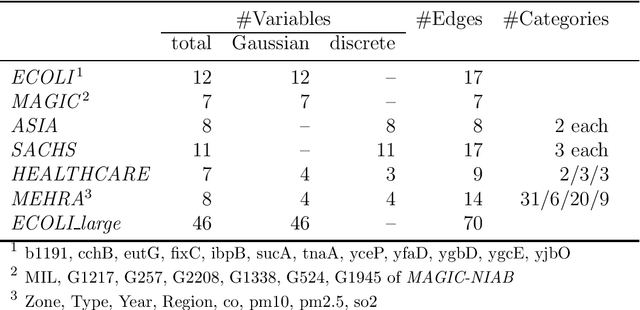
Causal discovery algorithms estimate causal graphs from observational data. This can provide a valuable complement to analyses focussing on the causal relation between individual treatment-outcome pairs. Constraint-based causal discovery algorithms rely on conditional independence testing when building the graph. Until recently, these algorithms have been unable to handle missing values. In this paper, we investigate two alternative solutions: Test-wise deletion and multiple imputation. We establish necessary and sufficient conditions for the recoverability of causal structures under test-wise deletion, and argue that multiple imputation is more challenging in the context of causal discovery than for estimation. We conduct an extensive comparison by simulating from benchmark causal graphs: As one might expect, we find that test-wise deletion and multiple imputation both clearly outperform list-wise deletion and single imputation. Crucially, our results further suggest that multiple imputation is especially useful in settings with a small number of either Gaussian or discrete variables, but when the dataset contains a mix of both neither method is uniformly best. The methods we compare include random forest imputation and a hybrid procedure combining test-wise deletion and multiple imputation. An application to data from the IDEFICS cohort study on diet- and lifestyle-related diseases in European children serves as an illustrating example.