Technical Report: Adaptive Control for Linearizable Systems Using On-Policy Reinforcement Learning

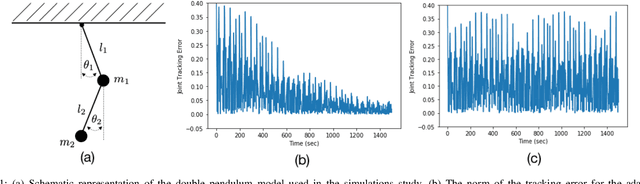
This paper proposes a framework for adaptively learning a feedback linearization-based tracking controller for an unknown system using discrete-time model-free policy-gradient parameter update rules. The primary advantage of the scheme over standard model-reference adaptive control techniques is that it does not require the learned inverse model to be invertible at all instances of time. This enables the use of general function approximators to approximate the linearizing controller for the system without having to worry about singularities. However, the discrete-time and stochastic nature of these algorithms precludes the direct application of standard machinery from the adaptive control literature to provide deterministic stability proofs for the system. Nevertheless, we leverage these techniques alongside tools from the stochastic approximation literature to demonstrate that with high probability the tracking and parameter errors concentrate near zero when a certain persistence of excitation condition is satisfied. A simulated example of a double pendulum demonstrates the utility of the proposed theory. 1

Exponentially Stable First Order Control on Matrix Lie Groups

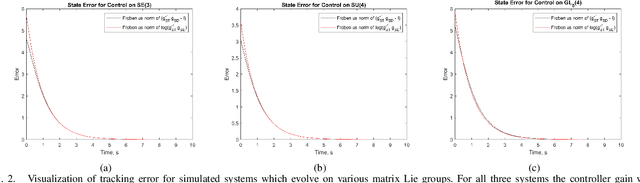
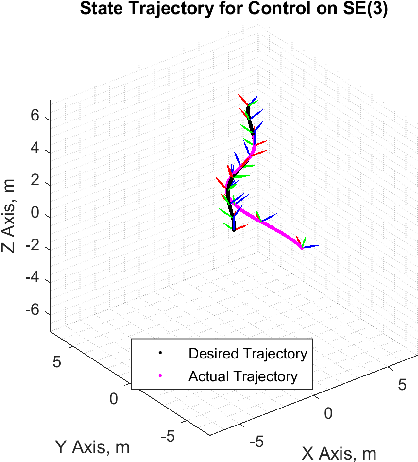
We present a novel first order controller for systems evolving on matrix Lie groups, a major use case of which is Cartesian velocity control on robot manipulators. This controller achieves global exponential trajectory tracking on a number of commonly used Lie groups including the Special Orthogonal Group SO(n), the Special Euclidean Group SE(n), and the General Linear Group over complex numbers GL(n, C). Additionally, this controller achieves local exponential trajectory tracking on all matrix Lie groups. We demonstrate the effectiveness of this controller in simulation on a number of different Lie groups as well as on hardware with a 7-DOF Sawyer robot arm.

Feedback Linearization for Unknown Systems via Reinforcement Learning

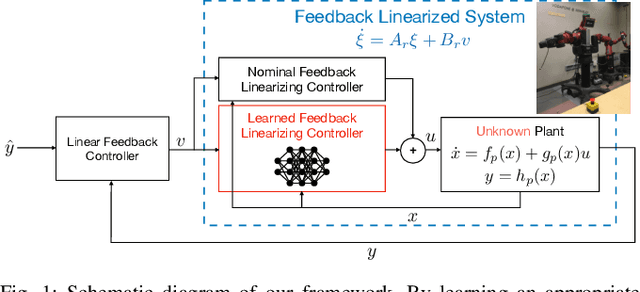
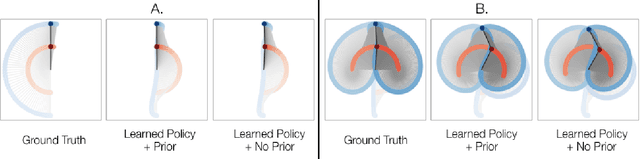
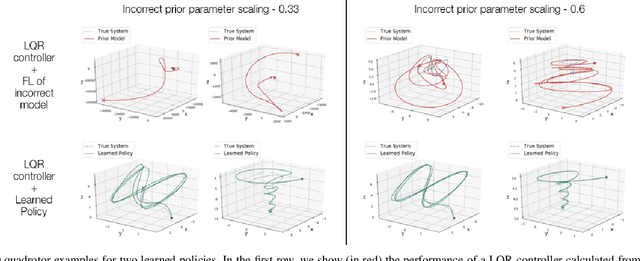
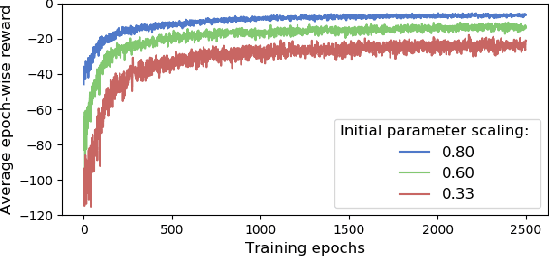
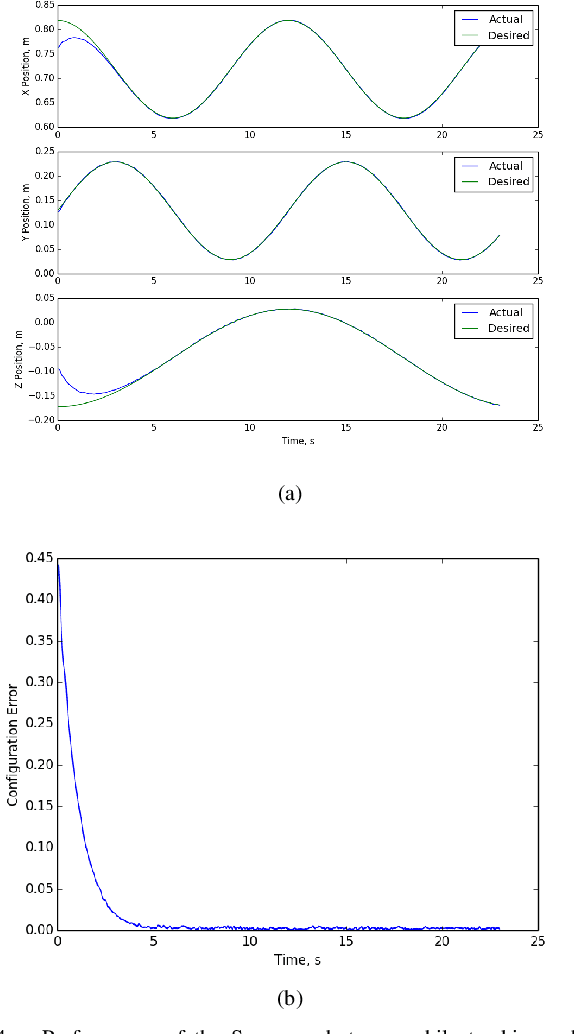
We present a novel approach to control design for nonlinear systems, which leverages reinforcement learning techniques to learn a linearizing controller for a physical plant with unknown dynamics. Feedback linearization is a technique from nonlinear control which renders the input-output dynamics of a nonlinear plant \emph{linear} under application of an appropriate feedback controller. Once a linearizing controller has been constructed, desired output trajectories for the nonlinear plant can be tracked using a variety of linear control techniques. A single learned policy then serves to track arbitrary desired reference signals provided by a higher-level planner. We present theoretical results which provide conditions under which the learning problem has a unique solution which exactly linearizes the plant. We demonstrate the performance of our approach on two simulated problems and a physical robotic platform. For the simulated environments, we observe that the learned feedback linearizing policies can achieve arbitrary tracking of reference trajectories for a fully actuated double pendulum and a 14 dimensional quadrotor. In hardware, we demonstrate that our approach significantly improves tracking performance on a 7-DOF Baxter robot after less than two hours of training.