Exponentially Stable First Order Control on Matrix Lie Groups

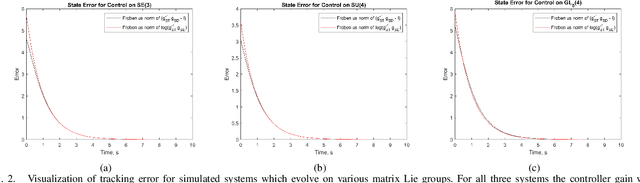
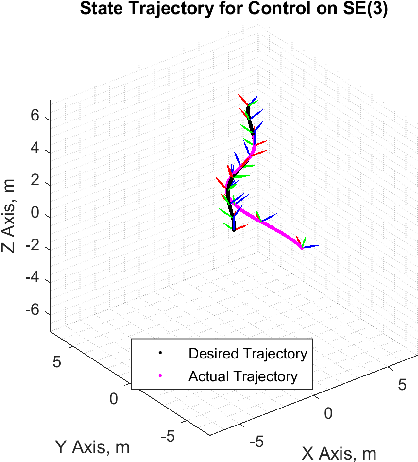
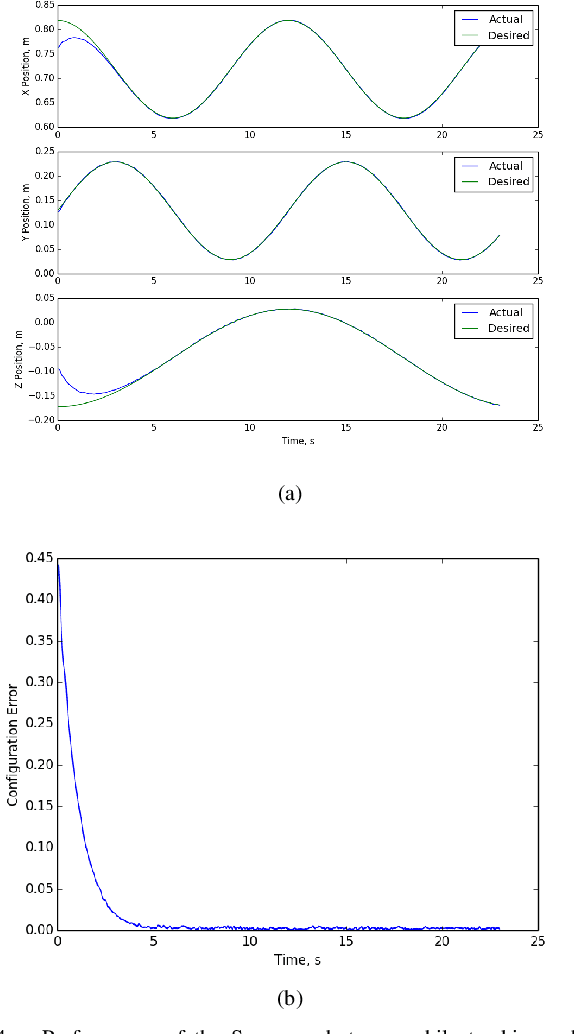
We present a novel first order controller for systems evolving on matrix Lie groups, a major use case of which is Cartesian velocity control on robot manipulators. This controller achieves global exponential trajectory tracking on a number of commonly used Lie groups including the Special Orthogonal Group SO(n), the Special Euclidean Group SE(n), and the General Linear Group over complex numbers GL(n, C). Additionally, this controller achieves local exponential trajectory tracking on all matrix Lie groups. We demonstrate the effectiveness of this controller in simulation on a number of different Lie groups as well as on hardware with a 7-DOF Sawyer robot arm.

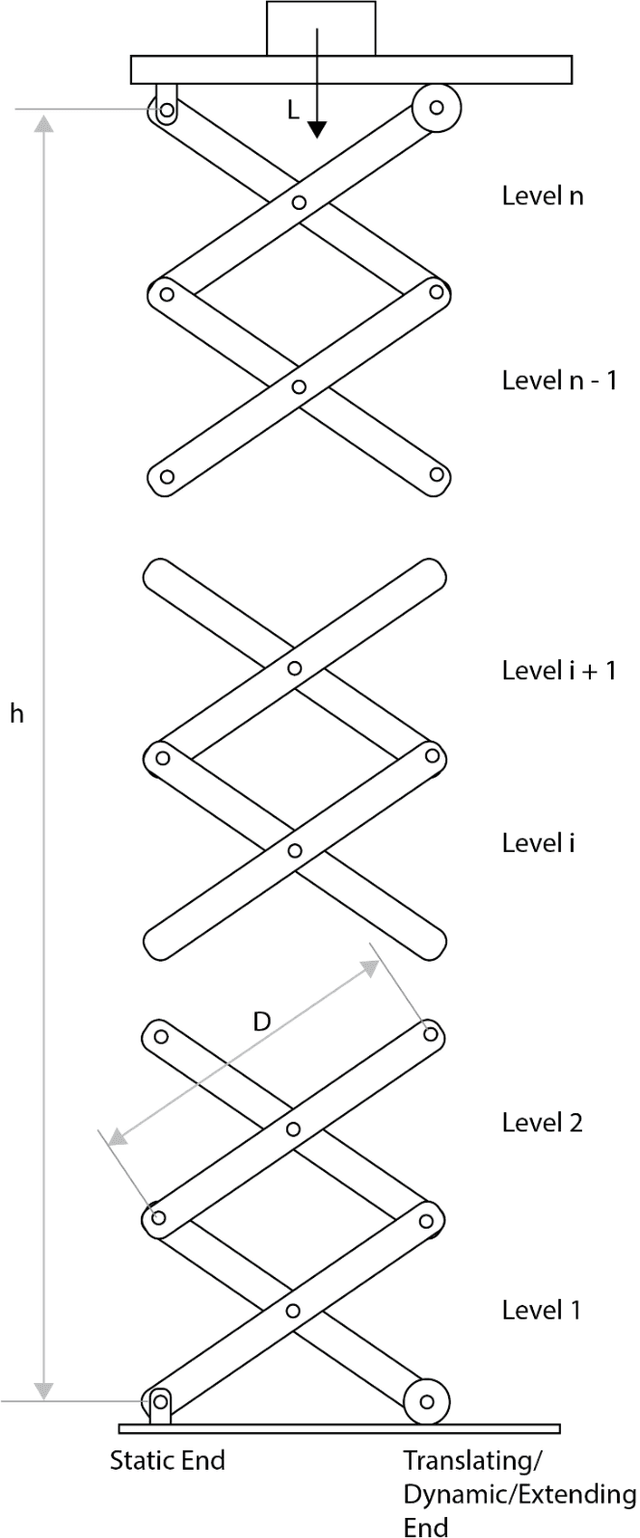
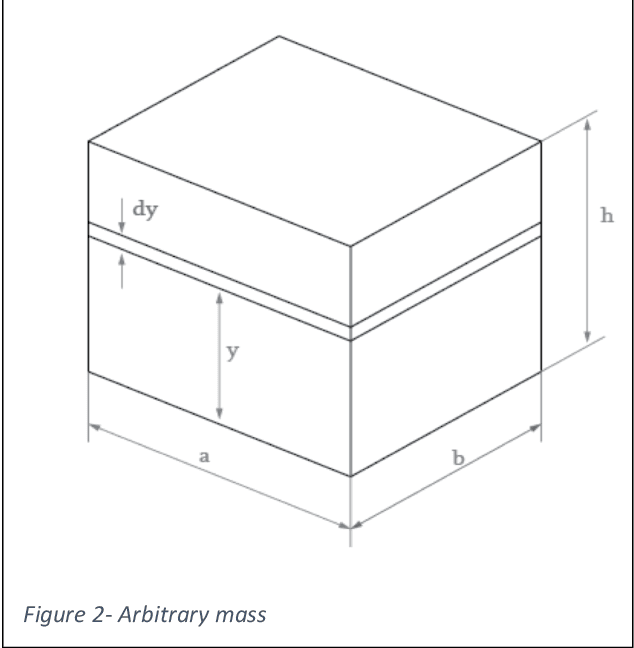
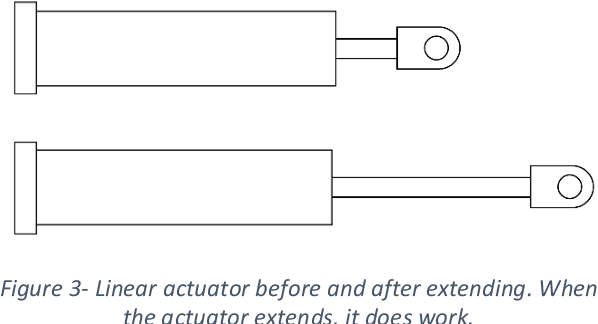
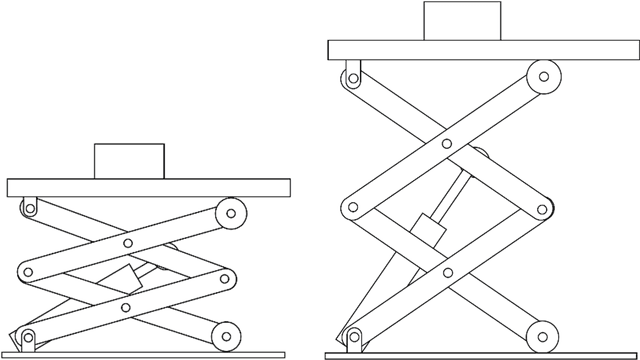
Deriving a Generalized, Actuator Position-Independent Expression for the Force Output of a Scissor Lift

Scissor lifts, a staple of mechanical design, especially in competitive robotics, are a type of linkage that can be used to raise a load to some height, when acted upon by some force, usually exerted by an actuator. The position of this actuator, however, can affect the mechanical advantage and velocity ratio of the system. Hence, there needs to be a concrete way to analytically compare different actuator positions. However, all current research into the analysis of scissor lifts either focusses only on the screw jack configuration, or derives separate force expressions for different actuator positions. This, once again, leaves the decision between different actuator positions to trial and error, since the expression to test the potency of the position can only be derived once the position is chosen. This paper proposes a derivation for a general force expression, in terms of a few carefully chosen position variables, which can be used to generate the force expression for any actuator position. Hence, this expression illustrates exactly how each of the position variables (called a, b and i in this paper, as defined later) affect the force output, and hence can be used to pick an appropriate actuator position, by choosing values for the position variables that give the desired result.