Exponentially Stable First Order Control on Matrix Lie Groups
Paper and Code
Apr 01, 2020
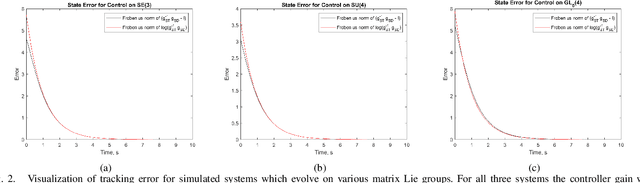
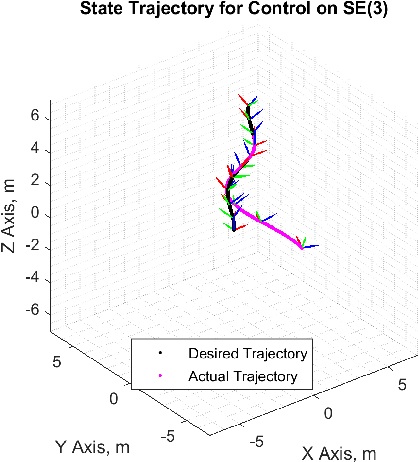
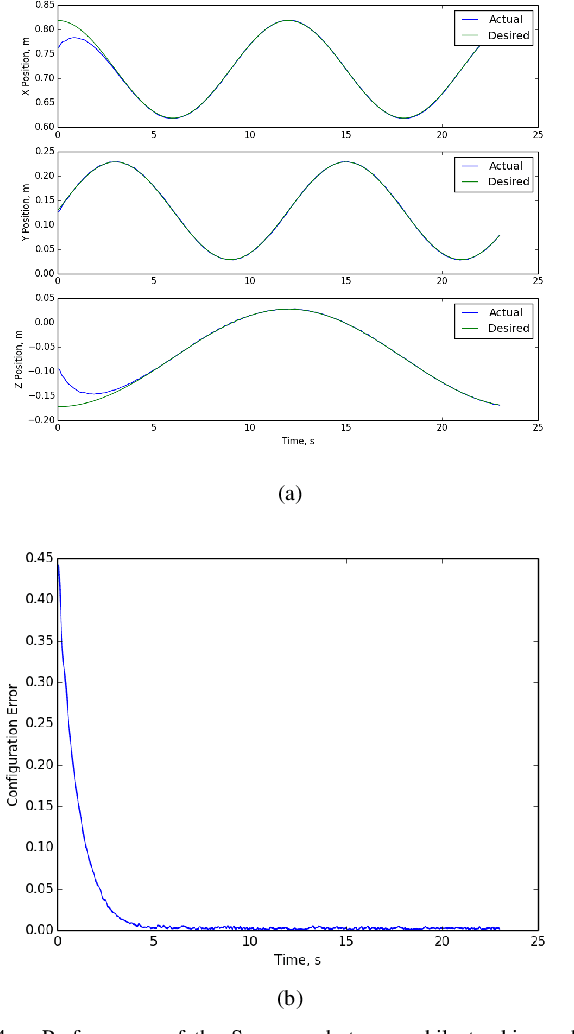
We present a novel first order controller for systems evolving on matrix Lie groups, a major use case of which is Cartesian velocity control on robot manipulators. This controller achieves global exponential trajectory tracking on a number of commonly used Lie groups including the Special Orthogonal Group SO(n), the Special Euclidean Group SE(n), and the General Linear Group over complex numbers GL(n, C). Additionally, this controller achieves local exponential trajectory tracking on all matrix Lie groups. We demonstrate the effectiveness of this controller in simulation on a number of different Lie groups as well as on hardware with a 7-DOF Sawyer robot arm.
* 8 pages, four figures, submitted to CDC 2020
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge