Modelling Commonsense Commonalities with Multi-Facet Concept Embeddings

Concept embeddings offer a practical and efficient mechanism for injecting commonsense knowledge into downstream tasks. Their core purpose is often not to predict the commonsense properties of concepts themselves, but rather to identify commonalities, i.e.\ sets of concepts which share some property of interest. Such commonalities are the basis for inductive generalisation, hence high-quality concept embeddings can make learning easier and more robust. Unfortunately, standard embeddings primarily reflect basic taxonomic categories, making them unsuitable for finding commonalities that refer to more specific aspects (e.g.\ the colour of objects or the materials they are made of). In this paper, we address this limitation by explicitly modelling the different facets of interest when learning concept embeddings. We show that this leads to embeddings which capture a more diverse range of commonsense properties, and consistently improves results in downstream tasks such as ultra-fine entity typing and ontology completion.

Ranking Entities along Conceptual Space Dimensions with LLMs: An Analysis of Fine-Tuning Strategies

Conceptual spaces represent entities in terms of their primitive semantic features. Such representations are highly valuable but they are notoriously difficult to learn, especially when it comes to modelling perceptual and subjective features. Distilling conceptual spaces from Large Language Models (LLMs) has recently emerged as a promising strategy. However, existing work has been limited to probing pre-trained LLMs using relatively simple zero-shot strategies. We focus in particular on the task of ranking entities according to a given conceptual space dimension. Unfortunately, we cannot directly fine-tune LLMs on this task, because ground truth rankings for conceptual space dimensions are rare. We therefore use more readily available features as training data and analyse whether the ranking capabilities of the resulting models transfer to perceptual and subjective features. We find that this is indeed the case, to some extent, but having perceptual and subjective features in the training data seems essential for achieving the best results. We furthermore find that pointwise ranking strategies are competitive against pairwise approaches, in defiance of common wisdom.

What do Deck Chairs and Sun Hats Have in Common? Uncovering Shared Properties in Large Concept Vocabularies

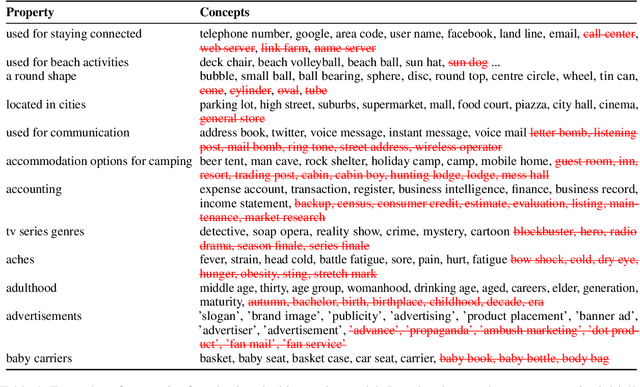
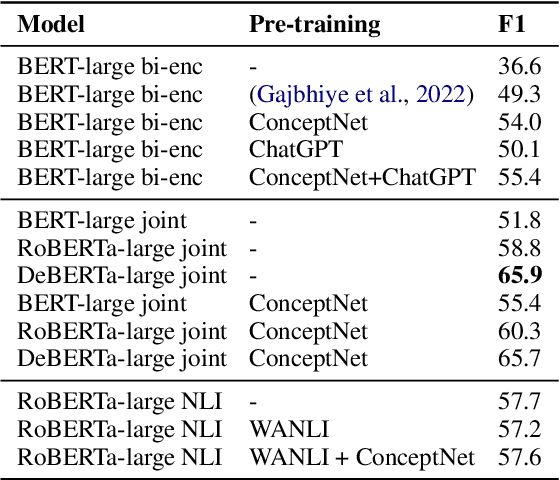
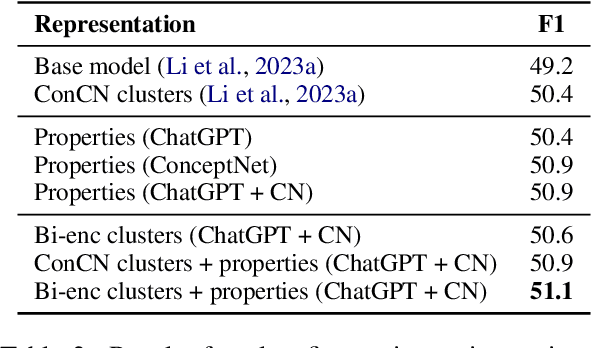
Concepts play a central role in many applications. This includes settings where concepts have to be modelled in the absence of sentence context. Previous work has therefore focused on distilling decontextualised concept embeddings from language models. But concepts can be modelled from different perspectives, whereas concept embeddings typically mostly capture taxonomic structure. To address this issue, we propose a strategy for identifying what different concepts, from a potentially large concept vocabulary, have in common with others. We then represent concepts in terms of the properties they share with the other concepts. To demonstrate the practical usefulness of this way of modelling concepts, we consider the task of ultra-fine entity typing, which is a challenging multi-label classification problem. We show that by augmenting the label set with shared properties, we can improve the performance of the state-of-the-art models for this task.

Cabbage Sweeter than Cake? Analysing the Potential of Large Language Models for Learning Conceptual Spaces

The theory of Conceptual Spaces is an influential cognitive-linguistic framework for representing the meaning of concepts. Conceptual spaces are constructed from a set of quality dimensions, which essentially correspond to primitive perceptual features (e.g. hue or size). These quality dimensions are usually learned from human judgements, which means that applications of conceptual spaces tend to be limited to narrow domains (e.g. modelling colour or taste). Encouraged by recent findings about the ability of Large Language Models (LLMs) to learn perceptually grounded representations, we explore the potential of such models for learning conceptual spaces. Our experiments show that LLMs can indeed be used for learning meaningful representations to some extent. However, we also find that fine-tuned models of the BERT family are able to match or even outperform the largest GPT-3 model, despite being 2 to 3 orders of magnitude smaller.