Initial Conditions from Galaxies: Machine-Learning Subgrid Correction to Standard Reconstruction

We present a hybrid method for reconstructing the primordial density from late-time halos and galaxies. Our approach involves two steps: (1) apply standard Baryon Acoustic Oscillation (BAO) reconstruction to recover the large-scale features in the primordial density field and (2) train a deep learning model to learn small-scale corrections on partitioned subgrids of the full volume. At inference, this correction is then convolved across the full survey volume, enabling scaling to large survey volumes. We train our method on both mock halo catalogs and mock galaxy catalogs in both configuration and redshift space from the Quijote $1(h^{-1}\,\mathrm{Gpc})^3$ simulation suite. When evaluated on held-out simulations, our combined approach significantly improves the reconstruction cross-correlation coefficient with the true initial density field and remains robust to moderate model misspecification. Additionally, we show that models trained on $1(h^{-1}\,\mathrm{Gpc})^3$ can be applied to larger boxes--e.g., $(3h^{-1}\,\mathrm{Gpc})^3$--without retraining. Finally, we perform a Fisher analysis on our method's recovery of the BAO peak, and find that it significantly improves the error on the acoustic scale relative to standard BAO reconstruction. Ultimately, this method robustly captures nonlinearities and bias without sacrificing large-scale accuracy, and its flexibility to handle arbitrarily large volumes without escalating computational requirements makes it especially promising for large-volume surveys like DESI.

Microcanonical Langevin Ensembles: Advancing the Sampling of Bayesian Neural Networks

Despite recent advances, sampling-based inference for Bayesian Neural Networks (BNNs) remains a significant challenge in probabilistic deep learning. While sampling-based approaches do not require a variational distribution assumption, current state-of-the-art samplers still struggle to navigate the complex and highly multimodal posteriors of BNNs. As a consequence, sampling still requires considerably longer inference times than non-Bayesian methods even for small neural networks, despite recent advances in making software implementations more efficient. Besides the difficulty of finding high-probability regions, the time until samplers provide sufficient exploration of these areas remains unpredictable. To tackle these challenges, we introduce an ensembling approach that leverages strategies from optimization and a recently proposed sampler called Microcanonical Langevin Monte Carlo (MCLMC) for efficient, robust and predictable sampling performance. Compared to approaches based on the state-of-the-art No-U-Turn Sampler, our approach delivers substantial speedups up to an order of magnitude, while maintaining or improving predictive performance and uncertainty quantification across diverse tasks and data modalities. The suggested Microcanonical Langevin Ensembles and modifications to MCLMC additionally enhance the method's predictability in resource requirements, facilitating easier parallelization. All in all, the proposed method offers a promising direction for practical, scalable inference for BNNs.

Deterministic Langevin Unconstrained Optimization with Normalizing Flows

We introduce a global, gradient-free surrogate optimization strategy for expensive black-box functions inspired by the Fokker-Planck and Langevin equations. These can be written as an optimization problem where the objective is the target function to maximize minus the logarithm of the current density of evaluated samples. This objective balances exploitation of the target objective with exploration of low-density regions. The method, Deterministic Langevin Optimization (DLO), relies on a Normalizing Flow density estimate to perform active learning and select proposal points for evaluation. This strategy differs qualitatively from the widely-used acquisition functions employed by Bayesian Optimization methods, and can accommodate a range of surrogate choices. We demonstrate superior or competitive progress toward objective optima on standard synthetic test functions, as well as on non-convex and multi-modal posteriors of moderate dimension. On real-world objectives, such as scientific and neural network hyperparameter optimization, DLO is competitive with state-of-the-art baselines.

Multiscale Flow for Robust and Optimal Cosmological Analysis

We propose Multiscale Flow, a generative Normalizing Flow that creates samples and models the field-level likelihood of two-dimensional cosmological data such as weak lensing. Multiscale Flow uses hierarchical decomposition of cosmological fields via a wavelet basis, and then models different wavelet components separately as Normalizing Flows. The log-likelihood of the original cosmological field can be recovered by summing over the log-likelihood of each wavelet term. This decomposition allows us to separate the information from different scales and identify distribution shifts in the data such as unknown scale-dependent systematics. The resulting likelihood analysis can not only identify these types of systematics, but can also be made optimal, in the sense that the Multiscale Flow can learn the full likelihood at the field without any dimensionality reduction. We apply Multiscale Flow to weak lensing mock datasets for cosmological inference, and show that it significantly outperforms traditional summary statistics such as power spectrum and peak counts, as well as novel Machine Learning based summary statistics such as scattering transform and convolutional neural networks. We further show that Multiscale Flow is able to identify distribution shifts not in the training data such as baryonic effects. Finally, we demonstrate that Multiscale Flow can be used to generate realistic samples of weak lensing data.

A Probabilistic Autoencoder for Type Ia Supernovae Spectral Time Series

We construct a physically-parameterized probabilistic autoencoder (PAE) to learn the intrinsic diversity of type Ia supernovae (SNe Ia) from a sparse set of spectral time series. The PAE is a two-stage generative model, composed of an Auto-Encoder (AE) which is interpreted probabilistically after training using a Normalizing Flow (NF). We demonstrate that the PAE learns a low-dimensional latent space that captures the nonlinear range of features that exists within the population, and can accurately model the spectral evolution of SNe Ia across the full range of wavelength and observation times directly from the data. By introducing a correlation penalty term and multi-stage training setup alongside our physically-parameterized network we show that intrinsic and extrinsic modes of variability can be separated during training, removing the need for the additional models to perform magnitude standardization. We then use our PAE in a number of downstream tasks on SNe Ia for increasingly precise cosmological analyses, including automatic detection of SN outliers, the generation of samples consistent with the data distribution, and solving the inverse problem in the presence of noisy and incomplete data to constrain cosmological distance measurements. We find that the optimal number of intrinsic model parameters appears to be three, in line with previous studies, and show that we can standardize our test sample of SNe Ia with an RMS of $0.091 \pm 0.010$ mag, which corresponds to $0.074 \pm 0.010$ mag if peculiar velocity contributions are removed. Trained models and codes are released at \href{https://github.com/georgestein/suPAErnova}{github.com/georgestein/suPAErnova}

Deterministic Langevin Monte Carlo with Normalizing Flows for Bayesian Inference

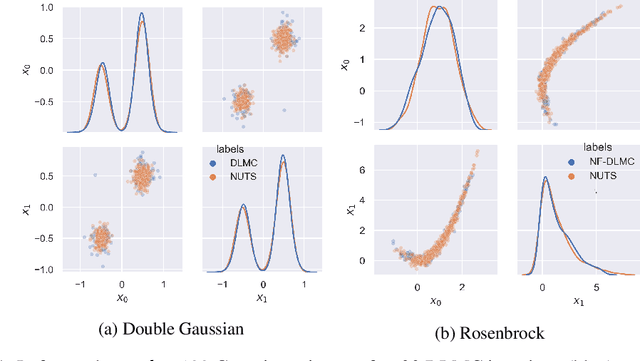
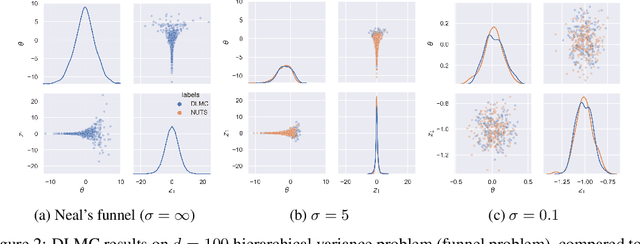
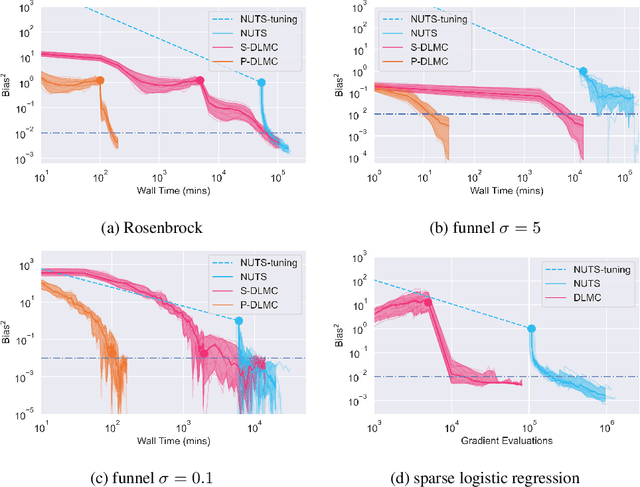
We propose a general purpose Bayesian inference algorithm for expensive likelihoods, replacing the stochastic term in the Langevin equation with a deterministic density gradient term. The particle density is evaluated from the current particle positions using a Normalizing Flow (NF), which is differentiable and has good generalization properties in high dimensions. We take advantage of NF preconditioning and NF based Metropolis-Hastings updates for a faster and unbiased convergence. We show on various examples that the method is competitive against state of the art sampling methods.

Translation and Rotation Equivariant Normalizing Flow (TRENF) for Optimal Cosmological Analysis

Our universe is homogeneous and isotropic, and its perturbations obey translation and rotation symmetry. In this work we develop Translation and Rotation Equivariant Normalizing Flow (TRENF), a generative Normalizing Flow (NF) model which explicitly incorporates these symmetries, defining the data likelihood via a sequence of Fourier space-based convolutions and pixel-wise nonlinear transforms. TRENF gives direct access to the high dimensional data likelihood p(x|y) as a function of the labels y, such as cosmological parameters. In contrast to traditional analyses based on summary statistics, the NF approach has no loss of information since it preserves the full dimensionality of the data. On Gaussian random fields, the TRENF likelihood agrees well with the analytical expression and saturates the Fisher information content in the labels y. On nonlinear cosmological overdensity fields from N-body simulations, TRENF leads to significant improvements in constraining power over the standard power spectrum summary statistic. TRENF is also a generative model of the data, and we show that TRENF samples agree well with the N-body simulations it trained on, and that the inverse mapping of the data agrees well with a Gaussian white noise both visually and on various summary statistics: when this is perfectly achieved the resulting p(x|y) likelihood analysis becomes optimal. Finally, we develop a generalization of this model that can handle effects that break the symmetry of the data, such as the survey mask, which enables likelihood analysis on data without periodic boundaries.

Unsupervised in-distribution anomaly detection of new physics through conditional density estimation

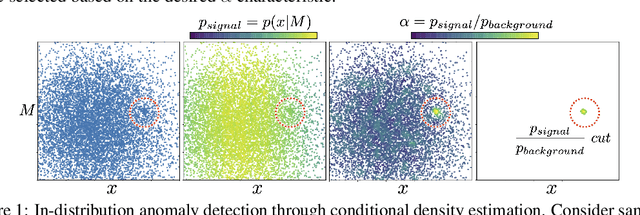
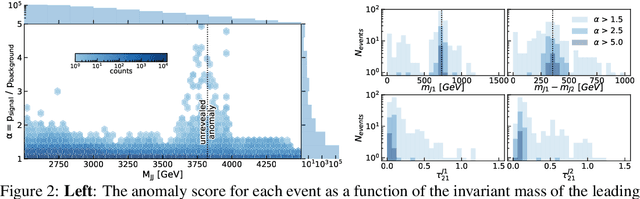
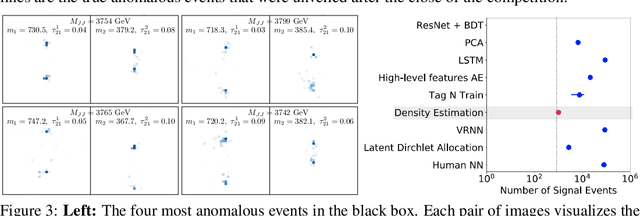
Anomaly detection is a key application of machine learning, but is generally focused on the detection of outlying samples in the low probability density regions of data. Here we instead present and motivate a method for unsupervised in-distribution anomaly detection using a conditional density estimator, designed to find unique, yet completely unknown, sets of samples residing in high probability density regions. We apply this method towards the detection of new physics in simulated Large Hadron Collider (LHC) particle collisions as part of the 2020 LHC Olympics blind challenge, and show how we detected a new particle appearing in only 0.08% of 1 million collision events. The results we present are our original blind submission to the 2020 LHC Olympics, where it achieved the state-of-the-art performance.

Learning effective physical laws for generating cosmological hydrodynamics with Lagrangian Deep Learning

The goal of generative models is to learn the intricate relations between the data to create new simulated data, but current approaches fail in very high dimensions. When the true data generating process is based on physical processes these impose symmetries and constraints, and the generative model can be created by learning an effective description of the underlying physics, which enables scaling of the generative model to very high dimensions. In this work we propose Lagrangian Deep Learning (LDL) for this purpose, applying it to learn outputs of cosmological hydrodynamical simulations. The model uses layers of Lagrangian displacements of particles describing the observables to learn the effective physical laws. The displacements are modeled as the gradient of an effective potential, which explicitly satisfies the translational and rotational invariance. The total number of learned parameters is only of order 10, and they can be viewed as effective theory parameters. We combine N-body solver FastPM with LDL and apply them to a wide range of cosmological outputs, from the dark matter to the stellar maps, gas density and temperature. The computational cost of LDL is nearly four orders of magnitude lower than the full hydrodynamical simulations, yet it outperforms it at the same resolution. We achieve this with only of order 10 layers from the initial conditions to the final output, in contrast to typical cosmological simulations with thousands of time steps. This opens up the possibility of analyzing cosmological observations entirely within this framework, without the need for large dark-matter simulations.

Sliced Iterative Generator

We introduce the Sliced Iterative Generator (SIG), an iterative generative model that is a Normalizing Flow (NF), but shares the advantages of Generative Adversarial Networks (GANs). The model is based on iterative Optimal Transport of a series of 1D slices through the data space, matching on each slice the probability distribution function (PDF) of the samples to the data. To improve the efficiency, the directions of the orthogonal slices are chosen to maximize the PDF difference between the generated samples and the data using Wasserstein distance at each iteration. A patch based approach is adopted to model the images in a hierarchical way, enabling the model to scale well to high dimensions. Unlike GANs, SIG has a NF structure and allows efficient likelihood evaluations that can be used in downstream tasks. We show that SIG is capable of generating realistic, high dimensional samples of images, achieving state of the art FID scores on MNIST and Fashion MNIST without any dimensionality reduction. It also has good Out of Distribution detection properties using the likelihood. To the best of our knowledge, SIG is the first iterative (greedy) deep learning algorithm that is competitive with the state of the art non-iterative generators in high dimensions. While SIG has a deep neural network architecture, the approach deviates significantly from the current deep learning paradigm, as it does not use concepts such as mini-batching, stochastic gradient descent, gradient back-propagation through deep layers, or non-convex loss function optimization. SIG is very insensitive to hyper-parameter tuning, making it a useful generator tool for ML experts and non-experts alike.