Multiscale Flow for Robust and Optimal Cosmological Analysis

We propose Multiscale Flow, a generative Normalizing Flow that creates samples and models the field-level likelihood of two-dimensional cosmological data such as weak lensing. Multiscale Flow uses hierarchical decomposition of cosmological fields via a wavelet basis, and then models different wavelet components separately as Normalizing Flows. The log-likelihood of the original cosmological field can be recovered by summing over the log-likelihood of each wavelet term. This decomposition allows us to separate the information from different scales and identify distribution shifts in the data such as unknown scale-dependent systematics. The resulting likelihood analysis can not only identify these types of systematics, but can also be made optimal, in the sense that the Multiscale Flow can learn the full likelihood at the field without any dimensionality reduction. We apply Multiscale Flow to weak lensing mock datasets for cosmological inference, and show that it significantly outperforms traditional summary statistics such as power spectrum and peak counts, as well as novel Machine Learning based summary statistics such as scattering transform and convolutional neural networks. We further show that Multiscale Flow is able to identify distribution shifts not in the training data such as baryonic effects. Finally, we demonstrate that Multiscale Flow can be used to generate realistic samples of weak lensing data.

Deterministic Langevin Monte Carlo with Normalizing Flows for Bayesian Inference

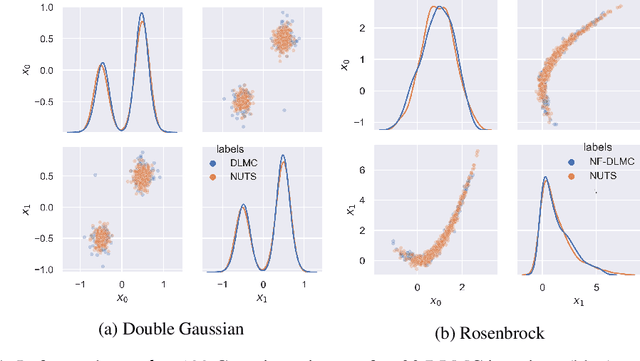
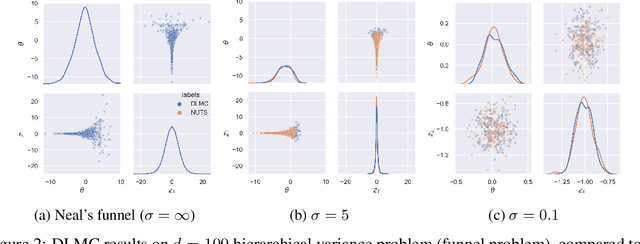
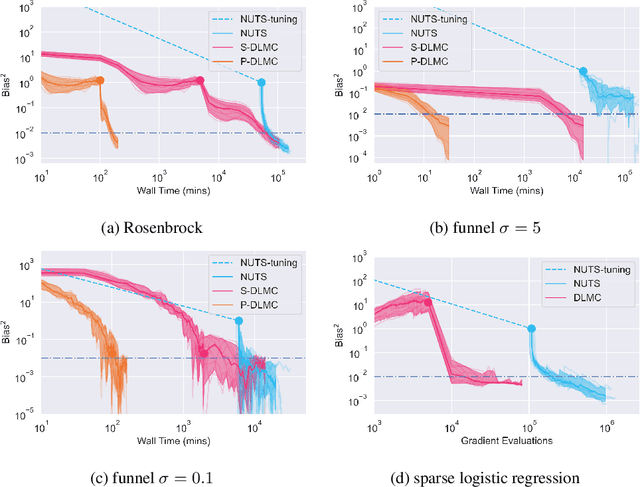
We propose a general purpose Bayesian inference algorithm for expensive likelihoods, replacing the stochastic term in the Langevin equation with a deterministic density gradient term. The particle density is evaluated from the current particle positions using a Normalizing Flow (NF), which is differentiable and has good generalization properties in high dimensions. We take advantage of NF preconditioning and NF based Metropolis-Hastings updates for a faster and unbiased convergence. We show on various examples that the method is competitive against state of the art sampling methods.

Translation and Rotation Equivariant Normalizing Flow (TRENF) for Optimal Cosmological Analysis

Our universe is homogeneous and isotropic, and its perturbations obey translation and rotation symmetry. In this work we develop Translation and Rotation Equivariant Normalizing Flow (TRENF), a generative Normalizing Flow (NF) model which explicitly incorporates these symmetries, defining the data likelihood via a sequence of Fourier space-based convolutions and pixel-wise nonlinear transforms. TRENF gives direct access to the high dimensional data likelihood p(x|y) as a function of the labels y, such as cosmological parameters. In contrast to traditional analyses based on summary statistics, the NF approach has no loss of information since it preserves the full dimensionality of the data. On Gaussian random fields, the TRENF likelihood agrees well with the analytical expression and saturates the Fisher information content in the labels y. On nonlinear cosmological overdensity fields from N-body simulations, TRENF leads to significant improvements in constraining power over the standard power spectrum summary statistic. TRENF is also a generative model of the data, and we show that TRENF samples agree well with the N-body simulations it trained on, and that the inverse mapping of the data agrees well with a Gaussian white noise both visually and on various summary statistics: when this is perfectly achieved the resulting p(x|y) likelihood analysis becomes optimal. Finally, we develop a generalization of this model that can handle effects that break the symmetry of the data, such as the survey mask, which enables likelihood analysis on data without periodic boundaries.

Unsupervised in-distribution anomaly detection of new physics through conditional density estimation

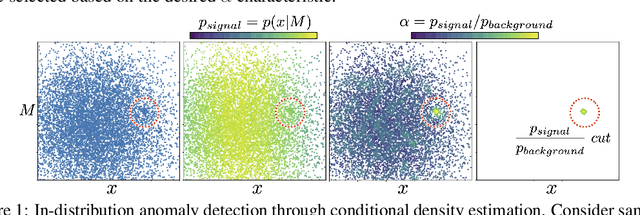
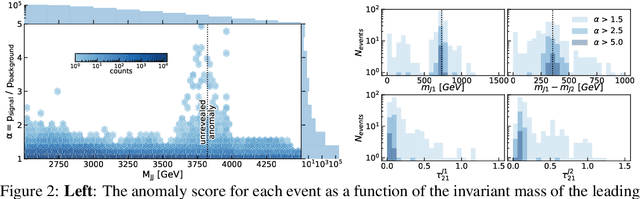
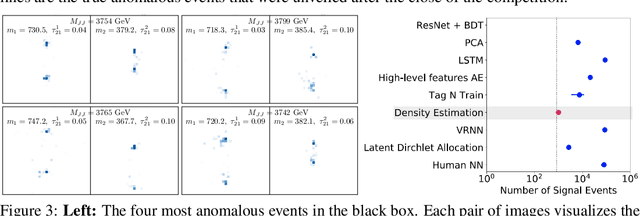
Anomaly detection is a key application of machine learning, but is generally focused on the detection of outlying samples in the low probability density regions of data. Here we instead present and motivate a method for unsupervised in-distribution anomaly detection using a conditional density estimator, designed to find unique, yet completely unknown, sets of samples residing in high probability density regions. We apply this method towards the detection of new physics in simulated Large Hadron Collider (LHC) particle collisions as part of the 2020 LHC Olympics blind challenge, and show how we detected a new particle appearing in only 0.08% of 1 million collision events. The results we present are our original blind submission to the 2020 LHC Olympics, where it achieved the state-of-the-art performance.

Learning effective physical laws for generating cosmological hydrodynamics with Lagrangian Deep Learning

The goal of generative models is to learn the intricate relations between the data to create new simulated data, but current approaches fail in very high dimensions. When the true data generating process is based on physical processes these impose symmetries and constraints, and the generative model can be created by learning an effective description of the underlying physics, which enables scaling of the generative model to very high dimensions. In this work we propose Lagrangian Deep Learning (LDL) for this purpose, applying it to learn outputs of cosmological hydrodynamical simulations. The model uses layers of Lagrangian displacements of particles describing the observables to learn the effective physical laws. The displacements are modeled as the gradient of an effective potential, which explicitly satisfies the translational and rotational invariance. The total number of learned parameters is only of order 10, and they can be viewed as effective theory parameters. We combine N-body solver FastPM with LDL and apply them to a wide range of cosmological outputs, from the dark matter to the stellar maps, gas density and temperature. The computational cost of LDL is nearly four orders of magnitude lower than the full hydrodynamical simulations, yet it outperforms it at the same resolution. We achieve this with only of order 10 layers from the initial conditions to the final output, in contrast to typical cosmological simulations with thousands of time steps. This opens up the possibility of analyzing cosmological observations entirely within this framework, without the need for large dark-matter simulations.

Sliced Iterative Generator

We introduce the Sliced Iterative Generator (SIG), an iterative generative model that is a Normalizing Flow (NF), but shares the advantages of Generative Adversarial Networks (GANs). The model is based on iterative Optimal Transport of a series of 1D slices through the data space, matching on each slice the probability distribution function (PDF) of the samples to the data. To improve the efficiency, the directions of the orthogonal slices are chosen to maximize the PDF difference between the generated samples and the data using Wasserstein distance at each iteration. A patch based approach is adopted to model the images in a hierarchical way, enabling the model to scale well to high dimensions. Unlike GANs, SIG has a NF structure and allows efficient likelihood evaluations that can be used in downstream tasks. We show that SIG is capable of generating realistic, high dimensional samples of images, achieving state of the art FID scores on MNIST and Fashion MNIST without any dimensionality reduction. It also has good Out of Distribution detection properties using the likelihood. To the best of our knowledge, SIG is the first iterative (greedy) deep learning algorithm that is competitive with the state of the art non-iterative generators in high dimensions. While SIG has a deep neural network architecture, the approach deviates significantly from the current deep learning paradigm, as it does not use concepts such as mini-batching, stochastic gradient descent, gradient back-propagation through deep layers, or non-convex loss function optimization. SIG is very insensitive to hyper-parameter tuning, making it a useful generator tool for ML experts and non-experts alike.