Deterministic Langevin Monte Carlo with Normalizing Flows for Bayesian Inference
Paper and Code
May 27, 2022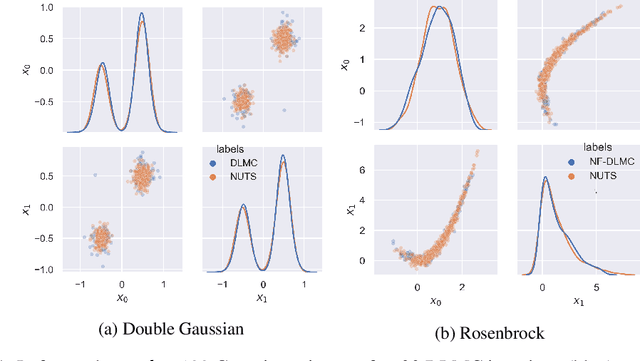
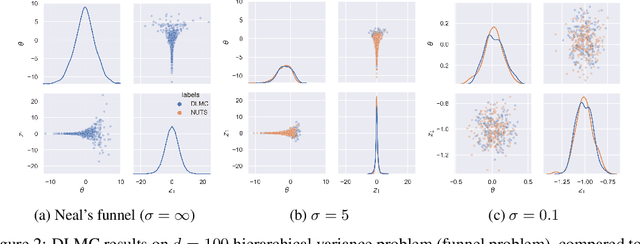
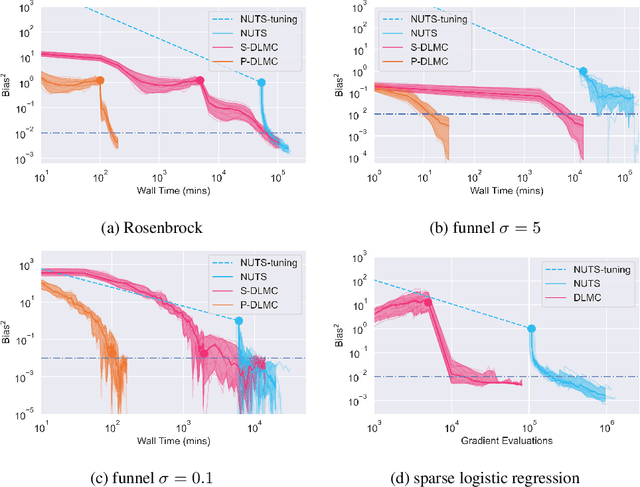

We propose a general purpose Bayesian inference algorithm for expensive likelihoods, replacing the stochastic term in the Langevin equation with a deterministic density gradient term. The particle density is evaluated from the current particle positions using a Normalizing Flow (NF), which is differentiable and has good generalization properties in high dimensions. We take advantage of NF preconditioning and NF based Metropolis-Hastings updates for a faster and unbiased convergence. We show on various examples that the method is competitive against state of the art sampling methods.
* 15 pages, 8 figures
View paper on
 OpenReview
OpenReview
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge