Zero Inflation as a Missing Data Problem: a Proxy-based Approach

A common type of zero-inflated data has certain true values incorrectly replaced by zeros due to data recording conventions (rare outcomes assumed to be absent) or details of data recording equipment (e.g. artificial zeros in gene expression data). Existing methods for zero-inflated data either fit the observed data likelihood via parametric mixture models that explicitly represent excess zeros, or aim to replace excess zeros by imputed values. If the goal of the analysis relies on knowing true data realizations, a particular challenge with zero-inflated data is identifiability, since it is difficult to correctly determine which observed zeros are real and which are inflated. This paper views zero-inflated data as a general type of missing data problem, where the observability indicator for a potentially censored variable is itself unobserved whenever a zero is recorded. We show that, without additional assumptions, target parameters involving a zero-inflated variable are not identified. However, if a proxy of the missingness indicator is observed, a modification of the effect restoration approach of Kuroki and Pearl allows identification and estimation, given the proxy-indicator relationship is known. If this relationship is unknown, our approach yields a partial identification strategy for sensitivity analysis. Specifically, we show that only certain proxy-indicator relationships are compatible with the observed data distribution. We give an analytic bound for this relationship in cases with a categorical outcome, which is sharp in certain models. For more complex cases, sharp numerical bounds may be computed using methods in Duarte et al.[2023]. We illustrate our method via simulation studies and a data application on central line-associated bloodstream infections (CLABSIs).

Global-Local Regularization Via Distributional Robustness

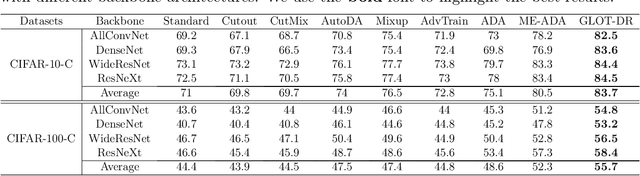
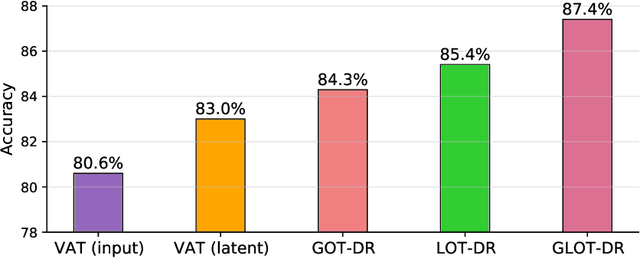
Despite superior performance in many situations, deep neural networks are often vulnerable to adversarial examples and distribution shifts, limiting model generalization ability in real-world applications. To alleviate these problems, recent approaches leverage distributional robustness optimization (DRO) to find the most challenging distribution, and then minimize loss function over this most challenging distribution. Regardless of achieving some improvements, these DRO approaches have some obvious limitations. First, they purely focus on local regularization to strengthen model robustness, missing a global regularization effect which is useful in many real-world applications (e.g., domain adaptation, domain generalization, and adversarial machine learning). Second, the loss functions in the existing DRO approaches operate in only the most challenging distribution, hence decouple with the original distribution, leading to a restrictive modeling capability. In this paper, we propose a novel regularization technique, following the veins of Wasserstein-based DRO framework. Specifically, we define a particular joint distribution and Wasserstein-based uncertainty, allowing us to couple the original and most challenging distributions for enhancing modeling capability and applying both local and global regularizations. Empirical studies on different learning problems demonstrate that our proposed approach significantly outperforms the existing regularization approaches in various domains: semi-supervised learning, domain adaptation, domain generalization, and adversarial machine learning.

On Learning Domain-Invariant Representations for Transfer Learning with Multiple Sources

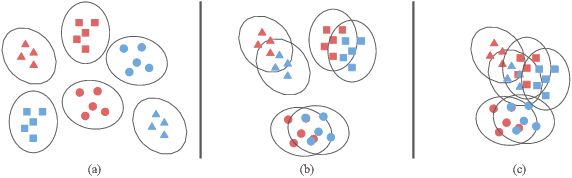
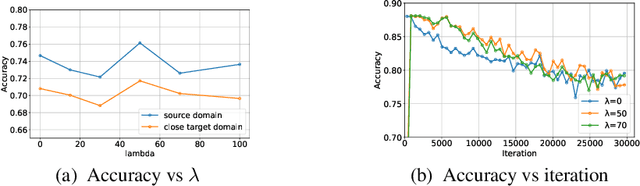
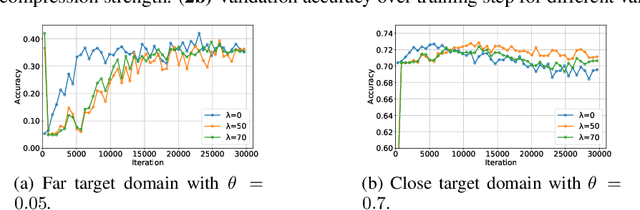
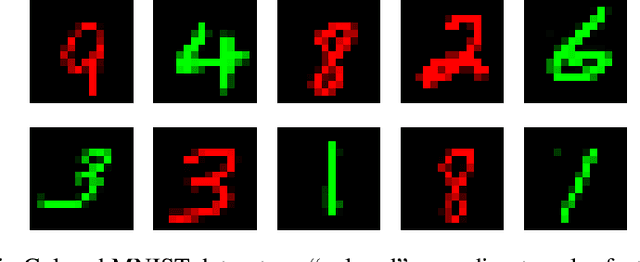
Domain adaptation (DA) benefits from the rigorous theoretical works that study its insightful characteristics and various aspects, e.g., learning domain-invariant representations and its trade-off. However, it seems not the case for the multiple source DA and domain generalization (DG) settings which are remarkably more complicated and sophisticated due to the involvement of multiple source domains and potential unavailability of target domain during training. In this paper, we develop novel upper-bounds for the target general loss which appeal to us to define two kinds of domain-invariant representations. We further study the pros and cons as well as the trade-offs of enforcing learning each domain-invariant representation. Finally, we conduct experiments to inspect the trade-off of these representations for offering practical hints regarding how to use them in practice and explore other interesting properties of our developed theory.