Global-Local Regularization Via Distributional Robustness

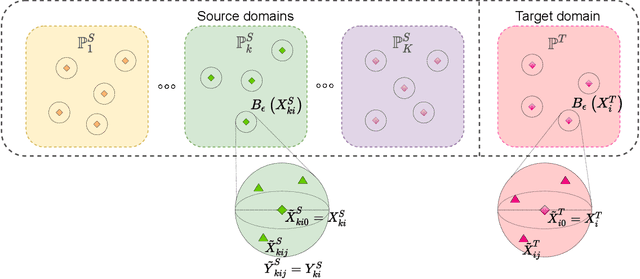
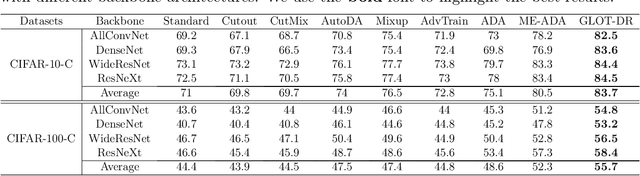
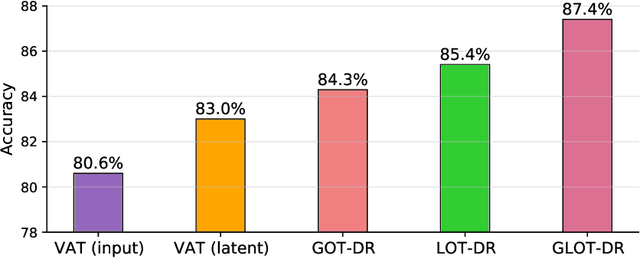
Despite superior performance in many situations, deep neural networks are often vulnerable to adversarial examples and distribution shifts, limiting model generalization ability in real-world applications. To alleviate these problems, recent approaches leverage distributional robustness optimization (DRO) to find the most challenging distribution, and then minimize loss function over this most challenging distribution. Regardless of achieving some improvements, these DRO approaches have some obvious limitations. First, they purely focus on local regularization to strengthen model robustness, missing a global regularization effect which is useful in many real-world applications (e.g., domain adaptation, domain generalization, and adversarial machine learning). Second, the loss functions in the existing DRO approaches operate in only the most challenging distribution, hence decouple with the original distribution, leading to a restrictive modeling capability. In this paper, we propose a novel regularization technique, following the veins of Wasserstein-based DRO framework. Specifically, we define a particular joint distribution and Wasserstein-based uncertainty, allowing us to couple the original and most challenging distributions for enhancing modeling capability and applying both local and global regularizations. Empirical studies on different learning problems demonstrate that our proposed approach significantly outperforms the existing regularization approaches in various domains: semi-supervised learning, domain adaptation, domain generalization, and adversarial machine learning.

A Unified Wasserstein Distributional Robustness Framework for Adversarial Training

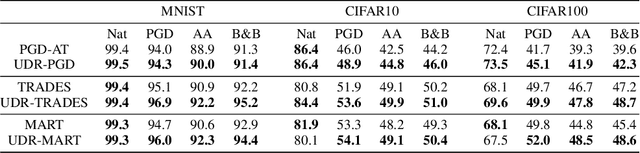
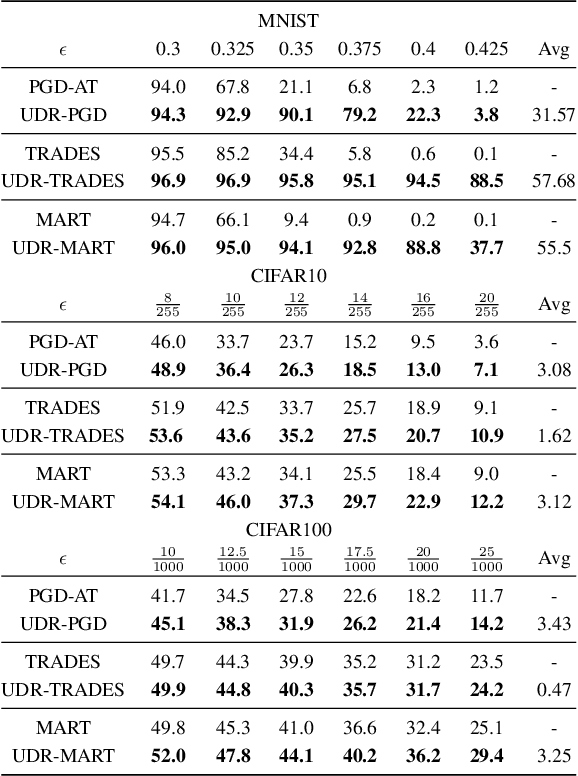
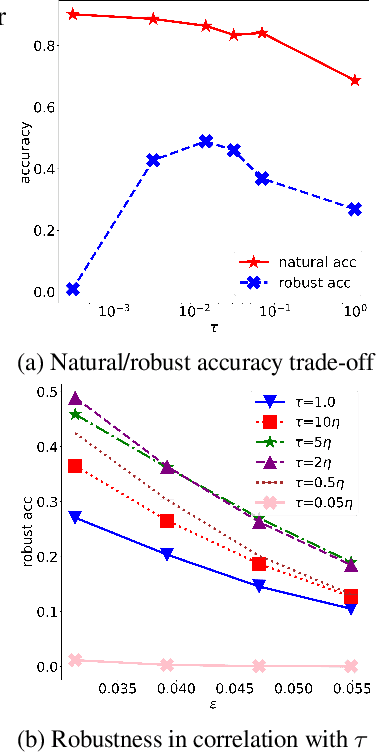
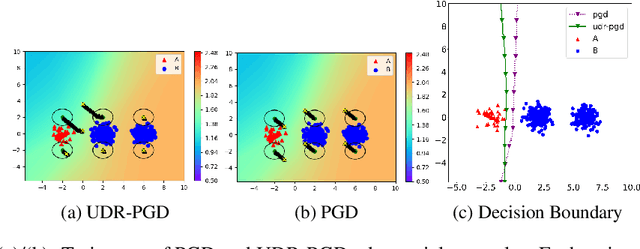
It is well-known that deep neural networks (DNNs) are susceptible to adversarial attacks, exposing a severe fragility of deep learning systems. As the result, adversarial training (AT) method, by incorporating adversarial examples during training, represents a natural and effective approach to strengthen the robustness of a DNN-based classifier. However, most AT-based methods, notably PGD-AT and TRADES, typically seek a pointwise adversary that generates the worst-case adversarial example by independently perturbing each data sample, as a way to "probe" the vulnerability of the classifier. Arguably, there are unexplored benefits in considering such adversarial effects from an entire distribution. To this end, this paper presents a unified framework that connects Wasserstein distributional robustness with current state-of-the-art AT methods. We introduce a new Wasserstein cost function and a new series of risk functions, with which we show that standard AT methods are special cases of their counterparts in our framework. This connection leads to an intuitive relaxation and generalization of existing AT methods and facilitates the development of a new family of distributional robustness AT-based algorithms. Extensive experiments show that our distributional robustness AT algorithms robustify further their standard AT counterparts in various settings.