Symbolic Regression of Data-Driven Reduced Order Model Closures for Under-Resolved, Convection-Dominated Flows

Data-driven closures correct the standard reduced order models (ROMs) to increase their accuracy in under-resolved, convection-dominated flows. There are two types of data-driven ROM closures in current use: (i) structural, with simple ansatzes (e.g., linear or quadratic); and (ii) machine learning-based, with neural network ansatzes. We propose a novel symbolic regression (SR) data-driven ROM closure strategy, which combines the advantages of current approaches and eliminates their drawbacks. As a result, the new data-driven SR closures yield ROMs that are interpretable, parsimonious, accurate, generalizable, and robust. To compare the data-driven SR-ROM closures with the structural and machine learning-based ROM closures, we consider the data-driven variational multiscale ROM framework and two under-resolved, convection-dominated test problems: the flow past a cylinder and the lid-driven cavity flow at Reynolds numbers Re = 10000, 15000, and 20000. This numerical investigation shows that the new data-driven SR-ROM closures yield more accurate and robust ROMs than the structural and machine learning ROM closures.

Physics Guided Machine Learning for Variational Multiscale Reduced Order Modeling

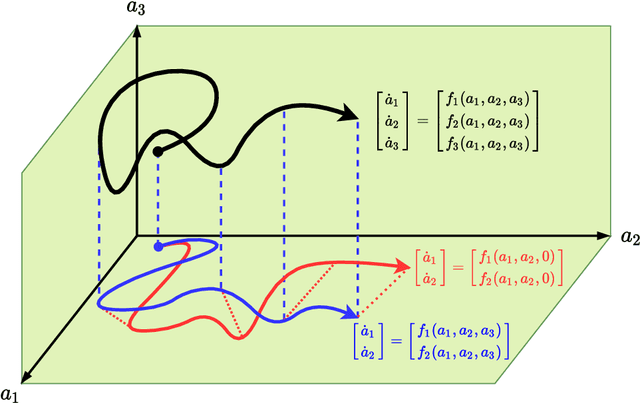
We propose a new physics guided machine learning (PGML) paradigm that leverages the variational multiscale (VMS) framework and available data to dramatically increase the accuracy of reduced order models (ROMs) at a modest computational cost. The hierarchical structure of the ROM basis and the VMS framework enable a natural separation of the resolved and unresolved ROM spatial scales. Modern PGML algorithms are used to construct novel models for the interaction among the resolved and unresolved ROM scales. Specifically, the new framework builds ROM operators that are closest to the true interaction terms in the VMS framework. Finally, machine learning is used to reduce the projection error and further increase the ROM accuracy. Our numerical experiments for a two-dimensional vorticity transport problem show that the novel PGML-VMS-ROM paradigm maintains the low computational cost of current ROMs, while significantly increasing the ROM accuracy.

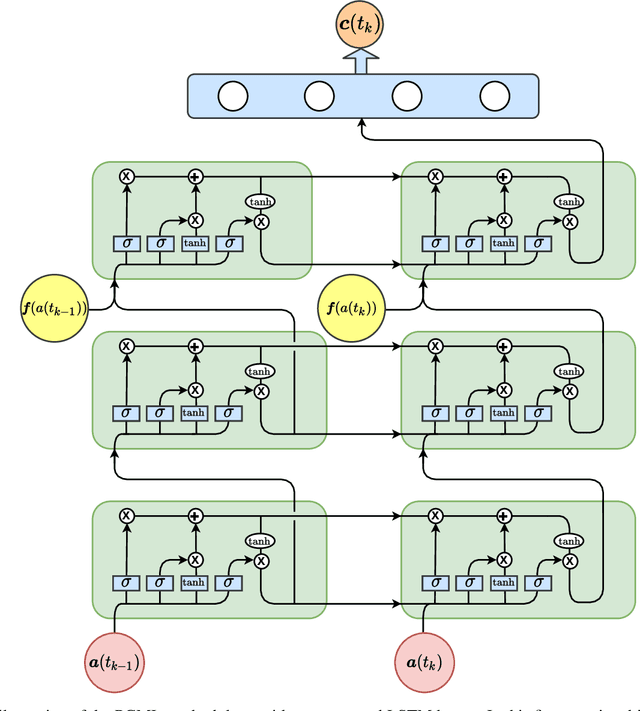
Nonlinear proper orthogonal decomposition for convection-dominated flows

Autoencoder techniques find increasingly common use in reduced order modeling as a means to create a latent space. This reduced order representation offers a modular data-driven modeling approach for nonlinear dynamical systems when integrated with a time series predictive model. In this letter, we put forth a nonlinear proper orthogonal decomposition (POD) framework, which is an end-to-end Galerkin-free model combining autoencoders with long short-term memory networks for dynamics. By eliminating the projection error due to the truncation of Galerkin models, a key enabler of the proposed nonintrusive approach is the kinematic construction of a nonlinear mapping between the full-rank expansion of the POD coefficients and the latent space where the dynamics evolve. We test our framework for model reduction of a convection-dominated system, which is generally challenging for reduced order models. Our approach not only improves the accuracy, but also significantly reduces the computational cost of training and testing.