A Multifidelity deep operator network approach to closure for multiscale systems

Projection-based reduced order models (PROMs) have shown promise in representing the behavior of multiscale systems using a small set of generalized (or latent) variables. Despite their success, PROMs can be susceptible to inaccuracies, even instabilities, due to the improper accounting of the interaction between the resolved and unresolved scales of the multiscale system (known as the closure problem). In the current work, we interpret closure as a multifidelity problem and use a multifidelity deep operator network (DeepONet) framework to address it. In addition, to enhance the stability and/or accuracy of the multifidelity-based closure, we employ the recently developed "in-the-loop" training approach from the literature on coupling physics and machine learning models. The resulting approach is tested on shock advection for the one-dimensional viscous Burgers equation and vortex merging for the two-dimensional Navier-Stokes equations. The numerical experiments show significant improvement of the predictive ability of the closure-corrected PROM over the un-corrected one both in the interpolative and the extrapolative regimes.

Physics Guided Machine Learning for Variational Multiscale Reduced Order Modeling

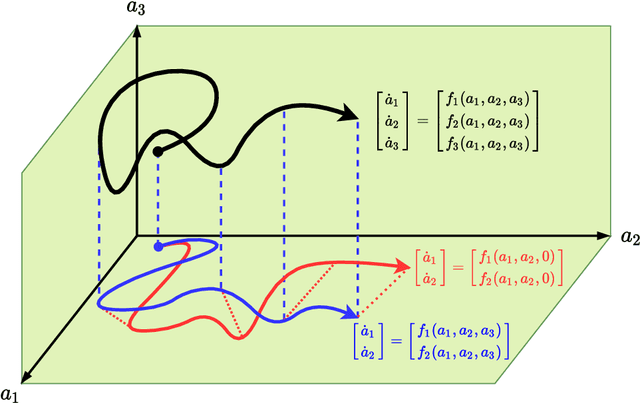
We propose a new physics guided machine learning (PGML) paradigm that leverages the variational multiscale (VMS) framework and available data to dramatically increase the accuracy of reduced order models (ROMs) at a modest computational cost. The hierarchical structure of the ROM basis and the VMS framework enable a natural separation of the resolved and unresolved ROM spatial scales. Modern PGML algorithms are used to construct novel models for the interaction among the resolved and unresolved ROM scales. Specifically, the new framework builds ROM operators that are closest to the true interaction terms in the VMS framework. Finally, machine learning is used to reduce the projection error and further increase the ROM accuracy. Our numerical experiments for a two-dimensional vorticity transport problem show that the novel PGML-VMS-ROM paradigm maintains the low computational cost of current ROMs, while significantly increasing the ROM accuracy.

Nonlinear proper orthogonal decomposition for convection-dominated flows

Autoencoder techniques find increasingly common use in reduced order modeling as a means to create a latent space. This reduced order representation offers a modular data-driven modeling approach for nonlinear dynamical systems when integrated with a time series predictive model. In this letter, we put forth a nonlinear proper orthogonal decomposition (POD) framework, which is an end-to-end Galerkin-free model combining autoencoders with long short-term memory networks for dynamics. By eliminating the projection error due to the truncation of Galerkin models, a key enabler of the proposed nonintrusive approach is the kinematic construction of a nonlinear mapping between the full-rank expansion of the POD coefficients and the latent space where the dynamics evolve. We test our framework for model reduction of a convection-dominated system, which is generally challenging for reduced order models. Our approach not only improves the accuracy, but also significantly reduces the computational cost of training and testing.

Interface learning of multiphysics and multiscale systems

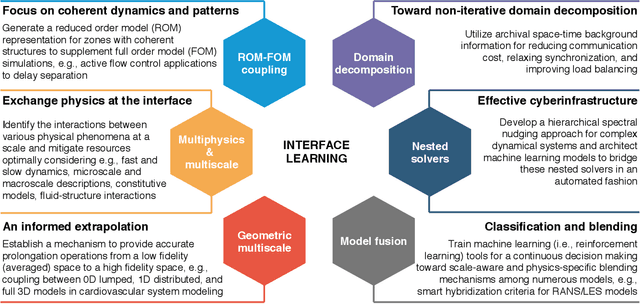
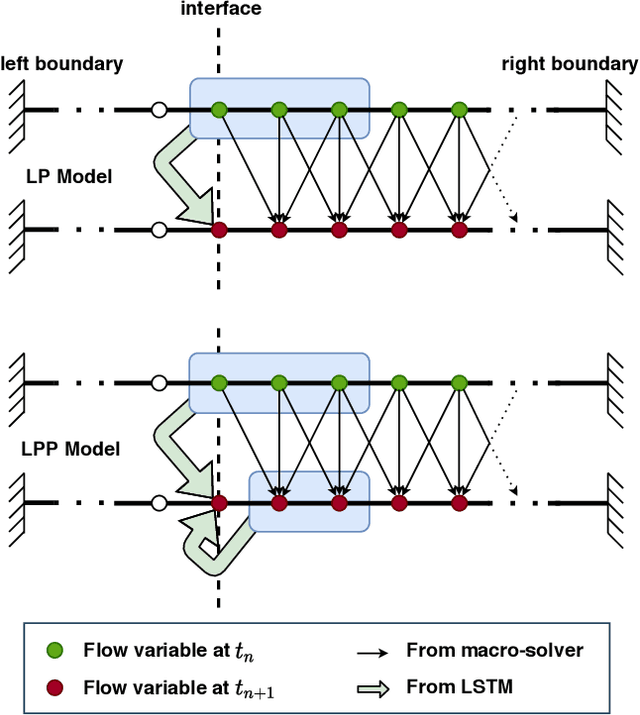
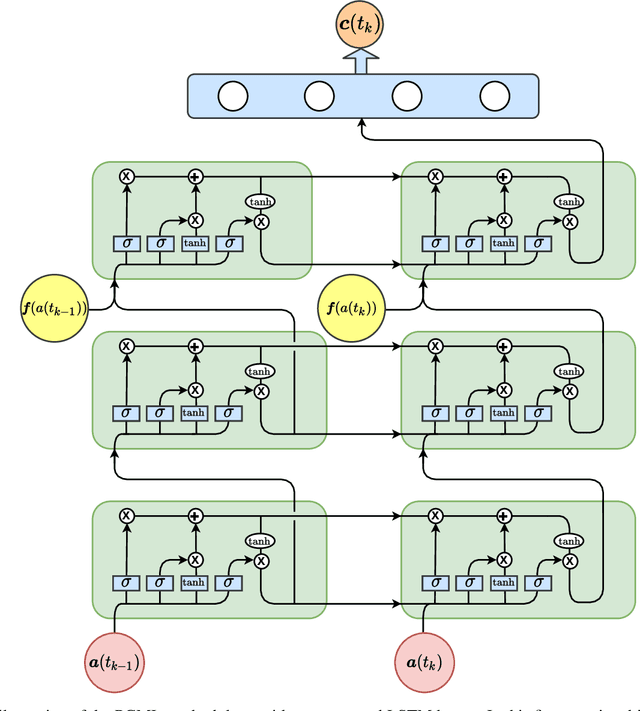
Complex natural or engineered systems comprise multiple characteristic scales, multiple spatiotemporal domains, and even multiple physical closure laws. To address such challenges, we introduce an interface learning paradigm and put forth a data-driven closure approach based on memory embedding to provide physically correct boundary conditions at the interface. Our findings in solving a bi-zonal nonlinear advection-diffusion equation show the proposed approach's promise for multiphysics and multiscale systems. We also highlight that high-performance computing environments can benefit from this methodology to reduce communication costs among processing units in emerging machine learning ready heterogeneous platforms toward exascale era.