MTNet: Learning modality-aware representation with transformer for RGBT tracking

The ability to learn robust multi-modality representation has played a critical role in the development of RGBT tracking. However, the regular fusion paradigm and the invariable tracking template remain restrictive to the feature interaction. In this paper, we propose a modality-aware tracker based on transformer, termed MTNet. Specifically, a modality-aware network is presented to explore modality-specific cues, which contains both channel aggregation and distribution module(CADM) and spatial similarity perception module (SSPM). A transformer fusion network is then applied to capture global dependencies to reinforce instance representations. To estimate the precise location and tackle the challenges, such as scale variation and deformation, we design a trident prediction head and a dynamic update strategy which jointly maintain a reliable template for facilitating inter-frame communication. Extensive experiments validate that the proposed method achieves satisfactory results compared with the state-of-the-art competitors on three RGBT benchmarks while reaching real-time speed.

Spatial-Temporal Human-Object Interaction Detection

In this paper, we propose a new instance-level human-object interaction detection task on videos called ST-HOID, which aims to distinguish fine-grained human-object interactions (HOIs) and the trajectories of subjects and objects. It is motivated by the fact that HOI is crucial for human-centric video content understanding. To solve ST-HOID, we propose a novel method consisting of an object trajectory detection module and an interaction reasoning module. Furthermore, we construct the first dataset named VidOR-HOID for ST-HOID evaluation, which contains 10,831 spatial-temporal HOI instances. We conduct extensive experiments to evaluate the effectiveness of our method. The experimental results demonstrate that our method outperforms the baselines generated by the state-of-the-art methods of image human-object interaction detection, video visual relation detection and video human-object interaction recognition.

RGB-D Tracking via Hierarchical Modality Aggregation and Distribution Network

The integration of dual-modal features has been pivotal in advancing RGB-Depth (RGB-D) tracking. However, current trackers are less efficient and focus solely on single-level features, resulting in weaker robustness in fusion and slower speeds that fail to meet the demands of real-world applications. In this paper, we introduce a novel network, denoted as HMAD (Hierarchical Modality Aggregation and Distribution), which addresses these challenges. HMAD leverages the distinct feature representation strengths of RGB and depth modalities, giving prominence to a hierarchical approach for feature distribution and fusion, thereby enhancing the robustness of RGB-D tracking. Experimental results on various RGB-D datasets demonstrate that HMAD achieves state-of-the-art performance. Moreover, real-world experiments further validate HMAD's capacity to effectively handle a spectrum of tracking challenges in real-time scenarios.

RGB-D Video Object Segmentation via Enhanced Multi-store Feature Memory

The RGB-Depth (RGB-D) Video Object Segmentation (VOS) aims to integrate the fine-grained texture information of RGB with the spatial geometric clues of depth modality, boosting the performance of segmentation. However, off-the-shelf RGB-D segmentation methods fail to fully explore cross-modal information and suffer from object drift during long-term prediction. In this paper, we propose a novel RGB-D VOS method via multi-store feature memory for robust segmentation. Specifically, we design the hierarchical modality selection and fusion, which adaptively combines features from both modalities. Additionally, we develop a segmentation refinement module that effectively utilizes the Segmentation Anything Model (SAM) to refine the segmentation mask, ensuring more reliable results as memory to guide subsequent segmentation tasks. By leveraging spatio-temporal embedding and modality embedding, mixed prompts and fused images are fed into SAM to unleash its potential in RGB-D VOS. Experimental results show that the proposed method achieves state-of-the-art performance on the latest RGB-D VOS benchmark.

KAN-SAM: Kolmogorov-Arnold Network Guided Segment Anything Model for RGB-T Salient Object Detection

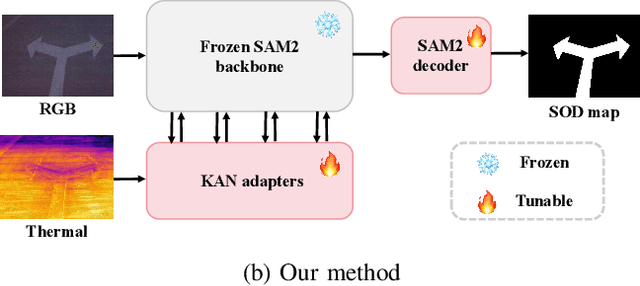
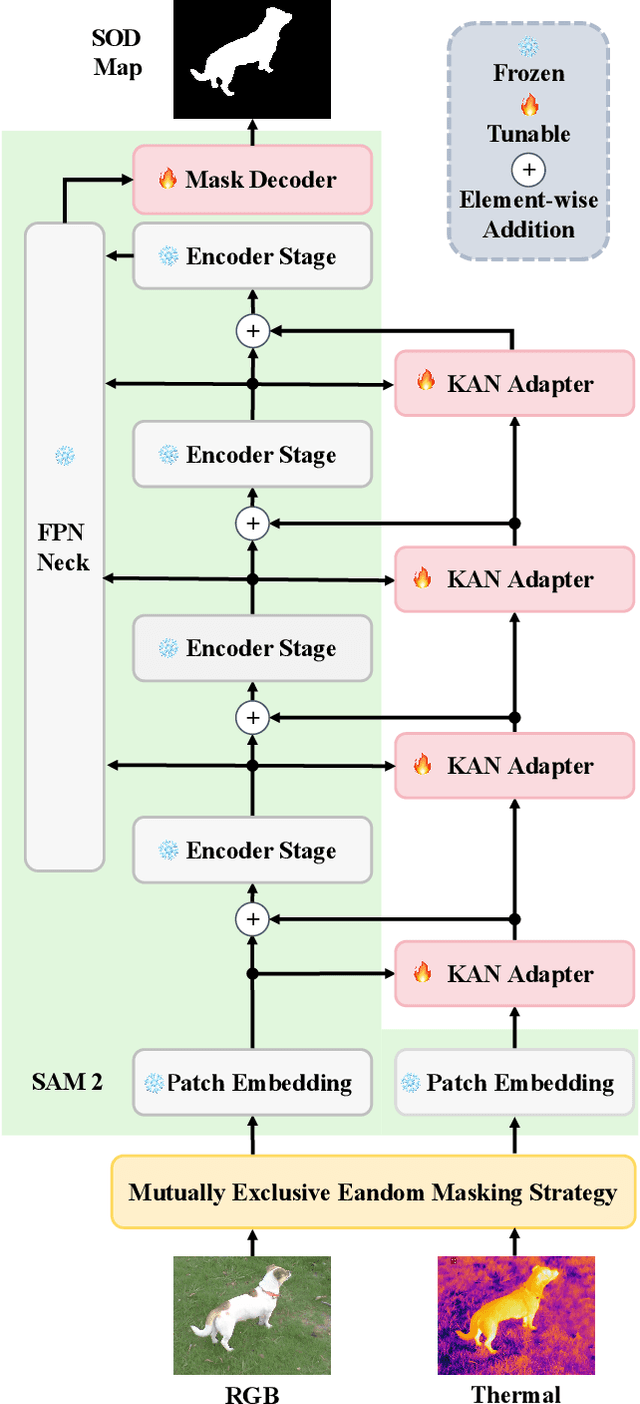
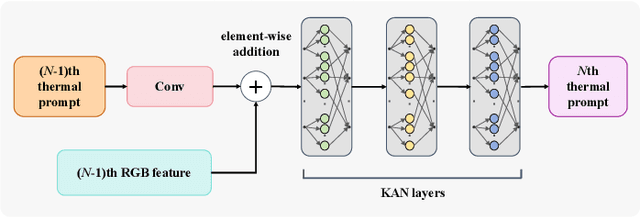
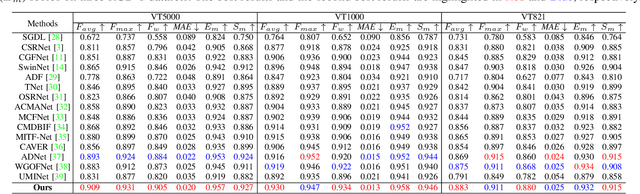
Existing RGB-thermal salient object detection (RGB-T SOD) methods aim to identify visually significant objects by leveraging both RGB and thermal modalities to enable robust performance in complex scenarios, but they often suffer from limited generalization due to the constrained diversity of available datasets and the inefficiencies in constructing multi-modal representations. In this paper, we propose a novel prompt learning-based RGB-T SOD method, named KAN-SAM, which reveals the potential of visual foundational models for RGB-T SOD tasks. Specifically, we extend Segment Anything Model 2 (SAM2) for RGB-T SOD by introducing thermal features as guiding prompts through efficient and accurate Kolmogorov-Arnold Network (KAN) adapters, which effectively enhance RGB representations and improve robustness. Furthermore, we introduce a mutually exclusive random masking strategy to reduce reliance on RGB data and improve generalization. Experimental results on benchmarks demonstrate superior performance over the state-of-the-art methods.

Fast Matrix Factorization with Non-Uniform Weights on Missing Data

Matrix factorization (MF) has been widely used to discover the low-rank structure and to predict the missing entries of data matrix. In many real-world learning systems, the data matrix can be very high-dimensional but sparse. This poses an imbalanced learning problem, since the scale of missing entries is usually much larger than that of observed entries, but they cannot be ignored due to the valuable negative signal. For efficiency concern, existing work typically applies a uniform weight on missing entries to allow a fast learning algorithm. However, this simplification will decrease modeling fidelity, resulting in suboptimal performance for downstream applications. In this work, we weight the missing data non-uniformly, and more generically, we allow any weighting strategy on the missing data. To address the efficiency challenge, we propose a fast learning method, for which the time complexity is determined by the number of observed entries in the data matrix, rather than the matrix size. The key idea is two-fold: 1) we apply truncated SVD on the weight matrix to get a more compact representation of the weights, and 2) we learn MF parameters with element-wise alternating least squares (eALS) and memorize the key intermediate variables to avoid repeating computations that are unnecessary. We conduct extensive experiments on two recommendation benchmarks, demonstrating the correctness, efficiency, and effectiveness of our fast eALS method.