A Dataset for Pharmacovigilance in German, French, and Japanese: Annotating Adverse Drug Reactions across Languages

User-generated data sources have gained significance in uncovering Adverse Drug Reactions (ADRs), with an increasing number of discussions occurring in the digital world. However, the existing clinical corpora predominantly revolve around scientific articles in English. This work presents a multilingual corpus of texts concerning ADRs gathered from diverse sources, including patient fora, social media, and clinical reports in German, French, and Japanese. Our corpus contains annotations covering 12 entity types, four attribute types, and 13 relation types. It contributes to the development of real-world multilingual language models for healthcare. We provide statistics to highlight certain challenges associated with the corpus and conduct preliminary experiments resulting in strong baselines for extracting entities and relations between these entities, both within and across languages.

Lower Bounds for the Total Variation Distance Between Arbitrary Distributions with Given Means and Variances

For arbitrary two probability measures on real d-space with given means and variances (covariance matrices), we provide lower bounds for their total variation distance.

Convex Optimization on Functionals of Probability Densities

In information theory, some optimization problems result in convex optimization problems on strictly convex functionals of probability densities. In this note, we study these problems and show conditions of minimizers and the uniqueness of the minimizer if there exist a minimizer.

A New Lower Bound for Kullback-Leibler Divergence Based on Hammersley-Chapman-Robbins Bound

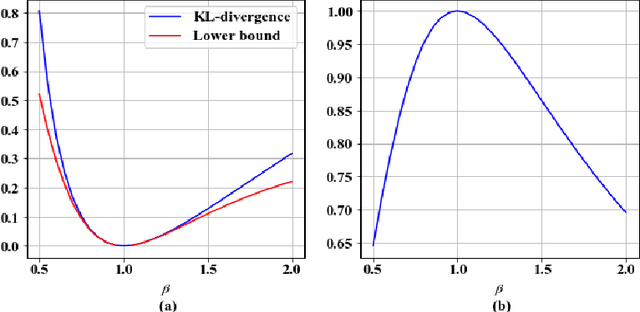
In this paper, we derive a useful lower bound for the Kullback-Leibler divergence (KL-divergence) based on the Hammersley-Chapman-Robbins bound (HCRB). The HCRB states that the variance of an estimator is bounded from below by the Chi-square divergence and the expectation value of the estimator. By using the relation between the KL-divergence and the Chi-square divergence, we show that the lower bound for the KL-divergence which only depends on the expectation value and the variance of a function we choose. This lower bound can also be derived from an information geometric approach. Furthermore, we show that the equality holds for the Bernoulli distributions and show that the inequality converges to the Cram\'{e}r-Rao bound when two distributions are very close. We also describe application examples and examples of numerical calculation.

Divergence Network: Graphical calculation method of divergence functions

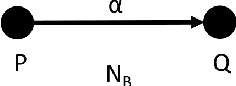
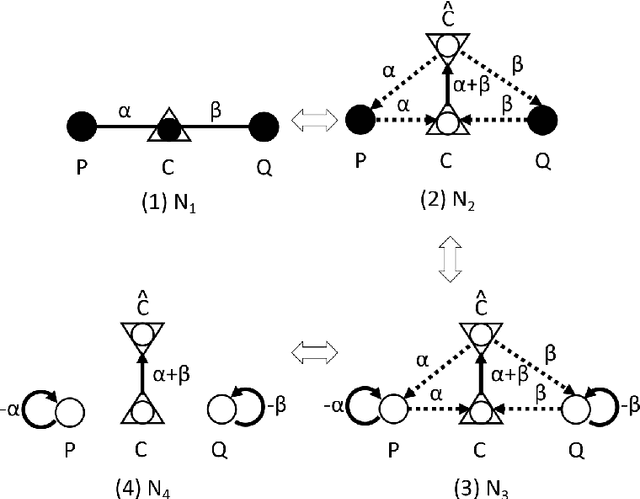
In this paper, we introduce directed networks called `divergence network' in order to perform graphical calculation of divergence functions. By using the divergence networks, we can easily understand the geometric meaning of calculation results and grasp relations among divergence functions intuitively.

Sum decomposition of divergence into three divergences

Divergence functions play a key role as to measure the discrepancy between two points in the field of machine learning, statistics and signal processing. Well-known divergences are the Bregman divergences, the Jensen divergences and the f-divergences. In this paper, we show that the symmetric Bregman divergence can be decomposed into the sum of two types of Jensen divergences and the Bregman divergence. Furthermore, applying this result, we show another sum decomposition of divergence is possible which includes f-divergences explicitly.

Generalized Bregman and Jensen divergences which include some f-divergences

In this paper, we introduce new classes of divergences by extending the definitions of the Bregman divergence and the skew Jensen divergence. These new divergence classes (g-Bregman divergence and skew g-Jensen divergence) satisfy some properties similar to the Bregman or skew Jensen divergence. We show these g-divergences include divergences which belong to a class of f-divergence (the Hellinger distance, the chi-square divergence and the alpha-divergence in addition to the Kullback-Leibler divergence). Moreover, we derive an inequality between the g-Bregman divergence and the skew g-Jensen divergence and show this inequality is a generalization of Lin's inequality.