Equilibrium Model with Anisotropy for Model-Based Reconstruction in Magnetic Particle Imaging

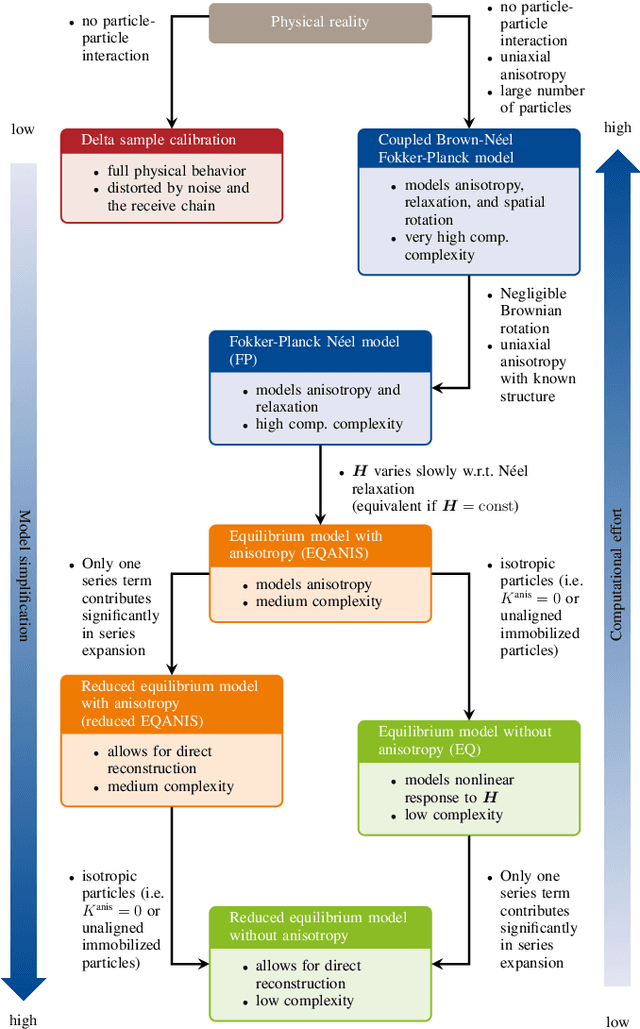
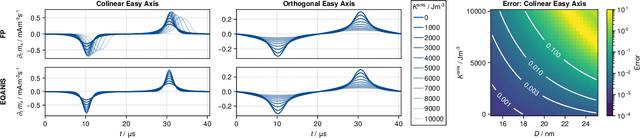
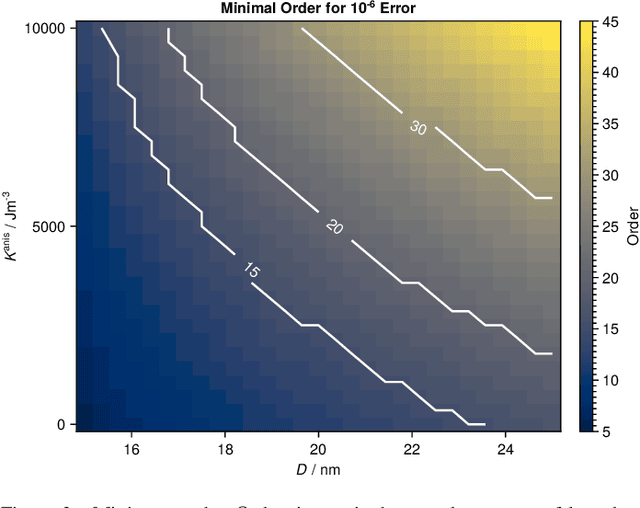
Magnetic particle imaging is a tracer-based tomographic imaging technique that allows the concentration of magnetic nanoparticles to be determined with high spatio-temporal resolution. To reconstruct an image of the tracer concentration, the magnetization dynamics of the particles must be accurately modeled. A popular ensemble model is based on solving the Fokker-Plank equation, taking into account either Brownian or N\'eel dynamics. The disadvantage of this model is that it is computationally expensive due to an underlying stiff differential equation. A simplified model is the equilibrium model, which can be evaluated directly but in most relevant cases it suffers from a non-negligible modeling error. In the present work, we investigate an extended version of the equilibrium model that can account for particle anisotropy. We show that this model can be expressed as a series of Bessel functions, which can be truncated based on a predefined accuracy, leading to very short computation times, which are about three orders of magnitude lower than equivalent Fokker-Planck computation times. We investigate the accuracy of the model for 2D Lissajous MPI sequences and show that the difference between the Fokker-Planck and the equilibrium model with anisotropy is sufficiently small so that the latter model can be used for image reconstruction on experimental data with only marginal loss of image quality, even compared to a system matrix-based reconstruction.

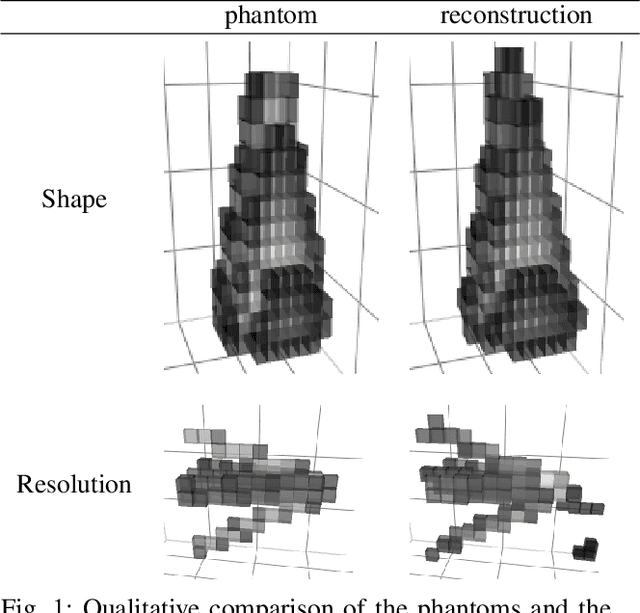
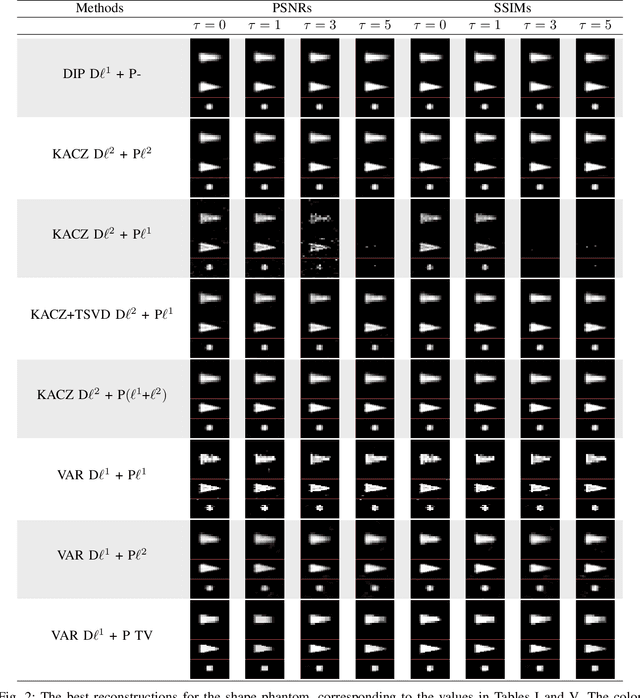
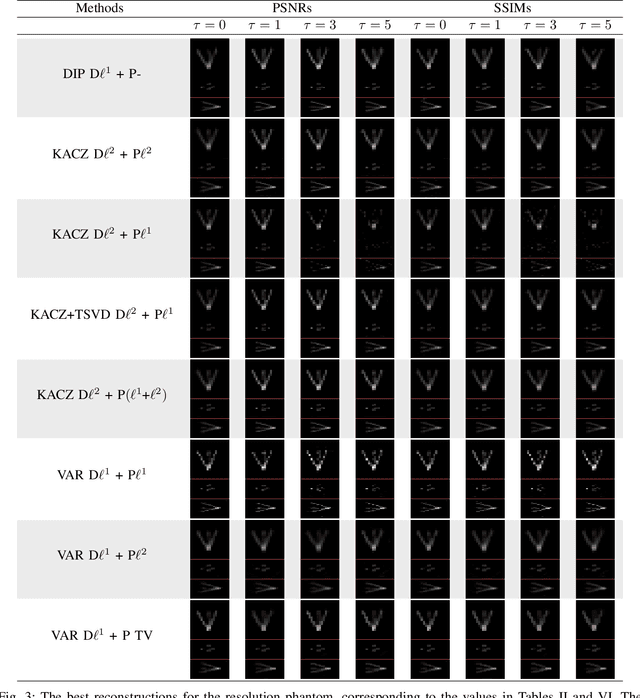
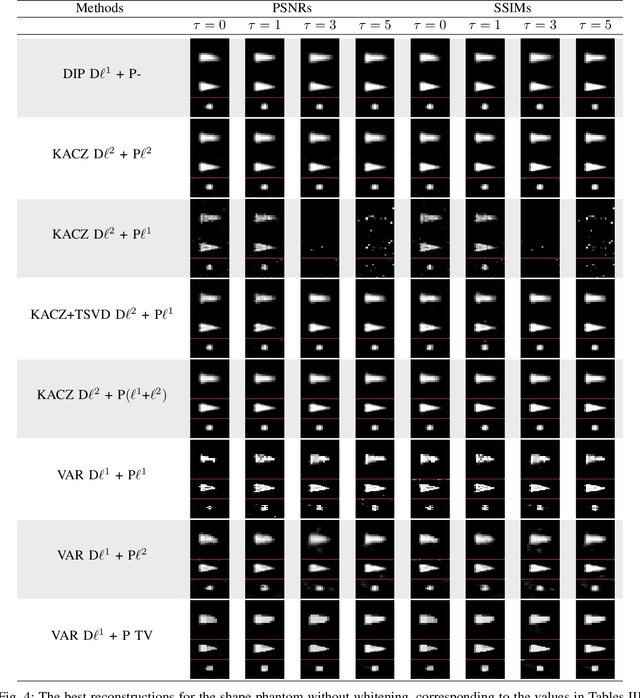
Deep image prior for 3D magnetic particle imaging: A quantitative comparison of regularization techniques on Open MPI dataset

Magnetic particle imaging (MPI) is an imaging modality exploiting the nonlinear magnetization behavior of (super-)paramagnetic nanoparticles to obtain a space- and often also time-dependent concentration of a tracer consisting of these nanoparticles. MPI has a continuously increasing number of potential medical applications. One prerequisite for successful performance in these applications is a proper solution to the image reconstruction problem. More classical methods from inverse problems theory, as well as novel approaches from the field of machine learning, have the potential to deliver high-quality reconstructions in MPI. We investigate a novel reconstruction approach based on a deep image prior, which builds on representing the solution by a deep neural network. Novel approaches, as well as variational and iterative regularization techniques, are compared quantitatively in terms of peak signal-to-noise ratios and structural similarity indices on the publicly available Open MPI dataset.

Regularization by architecture: A deep prior approach for inverse problems

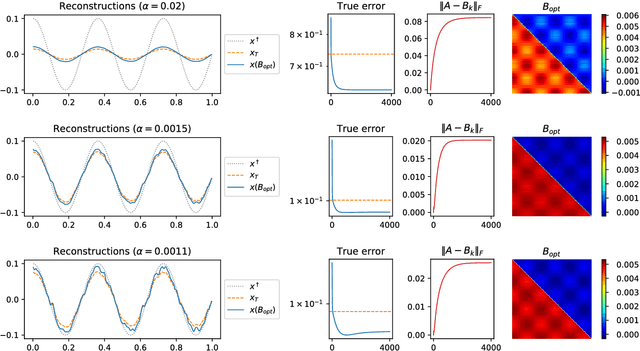
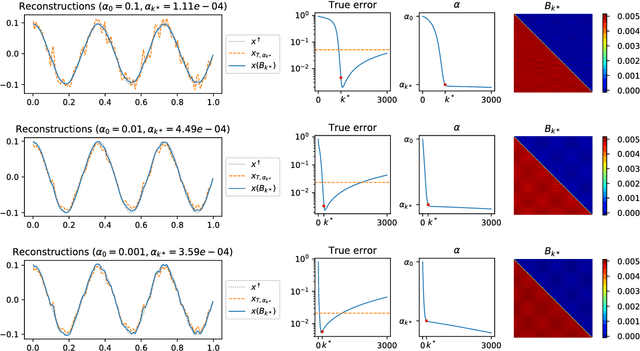
The present paper studies the so called deep image prior (DIP) technique in the context of inverse problems. DIP networks have been introduced recently for applications in image processing, also first experimental results for applying DIP to inverse problems have been reported. This paper aims at discussing different interpretations of DIP and to obtain analytic results for specific network designs and linear operators. The main contribution is to introduce the idea of viewing these approaches as the optimization of Tiknonov functionals rather than optimizing networks. Besides theoretical results, we present numerical verifications for an academic example (integration operator) as well as for the inverse problem of magnetic particle imaging (MPI). The reconstructions obtained by deep prior networks are compared with state of the art methods.