Efficient Chebyshev Reconstruction for the Anisotropic Equilibrium Model in Magnetic Particle Imaging

Magnetic Particle Imaging (MPI) is a tomographic imaging modality capable of real-time, high-sensitivity mapping of superparamagnetic iron oxide nanoparticles. Model-based image reconstruction provides an alternative to conventional methods that rely on a measured system matrix, eliminating the need for laborious calibration measurements. Nevertheless, model-based approaches must account for the complexities of the imaging chain to maintain high image quality. A recently proposed direct reconstruction method leverages weighted Chebyshev polynomials in the frequency domain, removing the need for a simulated system matrix. However, the underlying model neglects key physical effects, such as nanoparticle anisotropy, leading to distortions in reconstructed images. To mitigate these artifacts, an adapted direct Chebyshev reconstruction (DCR) method incorporates a spatially variant deconvolution step, significantly improving reconstruction accuracy at the cost of increased computational demands. In this work, we evaluate the adapted DCR on six experimental phantoms, demonstrating enhanced reconstruction quality in real measurements and achieving image fidelity comparable to or exceeding that of simulated system matrix reconstruction. Furthermore, we introduce an efficient approximation for the spatially variable deconvolution, reducing both runtime and memory consumption while maintaining accuracy. This method achieves computational complexity of O(N log N ), making it particularly beneficial for high-resolution and three-dimensional imaging. Our results highlight the potential of the adapted DCR approach for improving model-based MPI reconstruction in practical applications.

Equilibrium Model with Anisotropy for Model-Based Reconstruction in Magnetic Particle Imaging

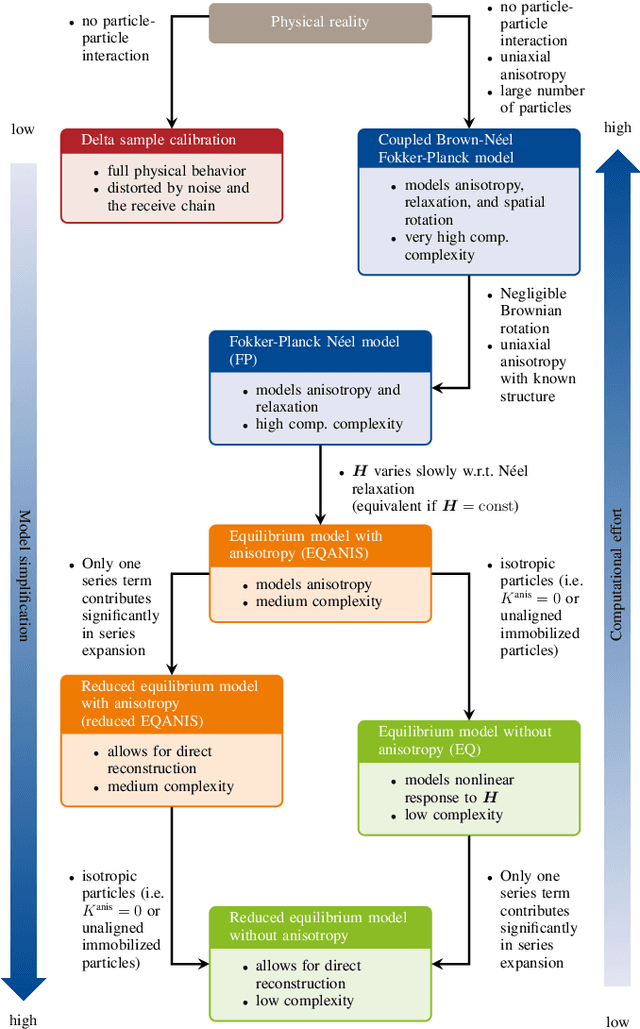
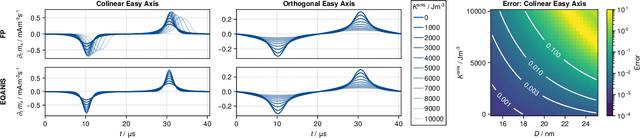
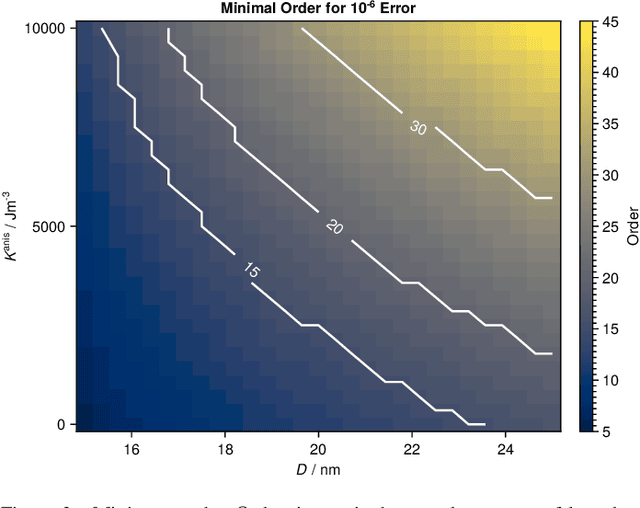
Magnetic particle imaging is a tracer-based tomographic imaging technique that allows the concentration of magnetic nanoparticles to be determined with high spatio-temporal resolution. To reconstruct an image of the tracer concentration, the magnetization dynamics of the particles must be accurately modeled. A popular ensemble model is based on solving the Fokker-Plank equation, taking into account either Brownian or N\'eel dynamics. The disadvantage of this model is that it is computationally expensive due to an underlying stiff differential equation. A simplified model is the equilibrium model, which can be evaluated directly but in most relevant cases it suffers from a non-negligible modeling error. In the present work, we investigate an extended version of the equilibrium model that can account for particle anisotropy. We show that this model can be expressed as a series of Bessel functions, which can be truncated based on a predefined accuracy, leading to very short computation times, which are about three orders of magnitude lower than equivalent Fokker-Planck computation times. We investigate the accuracy of the model for 2D Lissajous MPI sequences and show that the difference between the Fokker-Planck and the equilibrium model with anisotropy is sufficiently small so that the latter model can be used for image reconstruction on experimental data with only marginal loss of image quality, even compared to a system matrix-based reconstruction.