Equilibrium Model with Anisotropy for Model-Based Reconstruction in Magnetic Particle Imaging
Paper and Code
Mar 01, 2024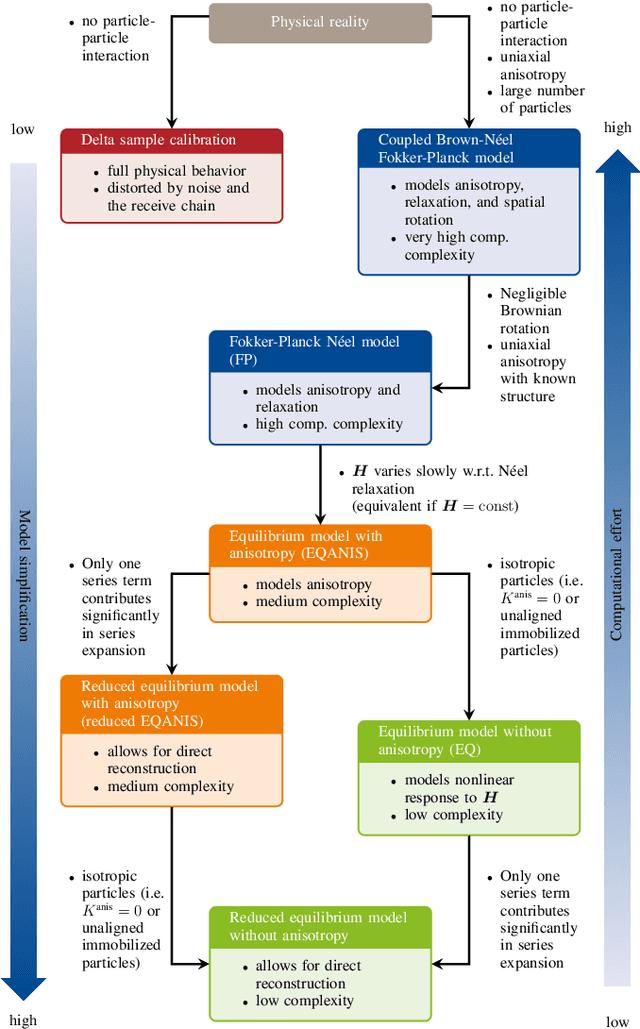
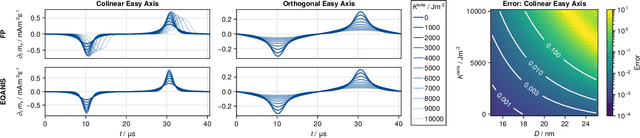
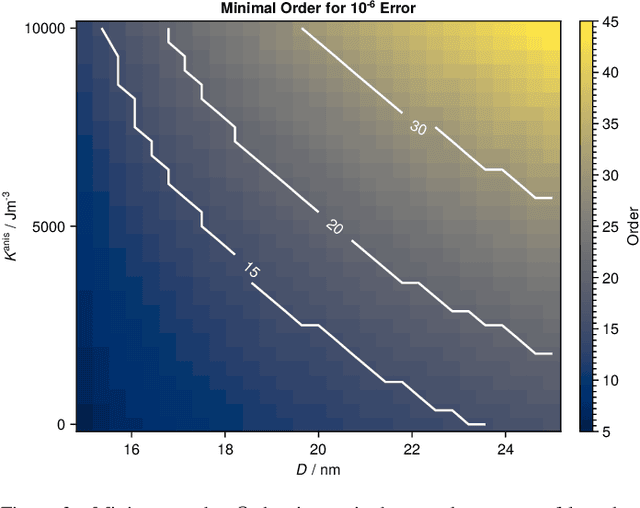

Magnetic particle imaging is a tracer-based tomographic imaging technique that allows the concentration of magnetic nanoparticles to be determined with high spatio-temporal resolution. To reconstruct an image of the tracer concentration, the magnetization dynamics of the particles must be accurately modeled. A popular ensemble model is based on solving the Fokker-Plank equation, taking into account either Brownian or N\'eel dynamics. The disadvantage of this model is that it is computationally expensive due to an underlying stiff differential equation. A simplified model is the equilibrium model, which can be evaluated directly but in most relevant cases it suffers from a non-negligible modeling error. In the present work, we investigate an extended version of the equilibrium model that can account for particle anisotropy. We show that this model can be expressed as a series of Bessel functions, which can be truncated based on a predefined accuracy, leading to very short computation times, which are about three orders of magnitude lower than equivalent Fokker-Planck computation times. We investigate the accuracy of the model for 2D Lissajous MPI sequences and show that the difference between the Fokker-Planck and the equilibrium model with anisotropy is sufficiently small so that the latter model can be used for image reconstruction on experimental data with only marginal loss of image quality, even compared to a system matrix-based reconstruction.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge