Linear Differential Games for Cooperative Behavior Planning of Autonomous Vehicles Using Mixed-Integer Programming

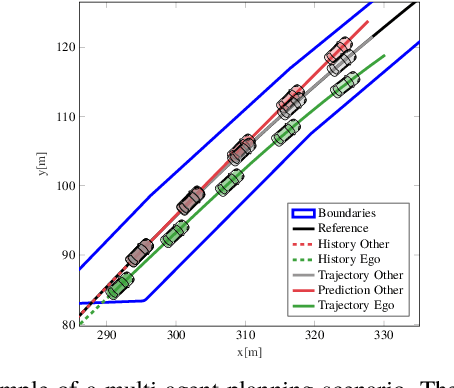
Cooperatively planning for multiple agents has been proposed as a promising method for strategic and motion planning for automated vehicles. By taking into account the intent of every agent, the ego agent can incorporate future interactions with human-driven vehicles into its planning. The problem is often formulated as a multi-agent game and solved using iterative algorithms operating on a discretized action or state space. Even if converging to a Nash equilibrium, the result will often be only sub-optimal. In this paper, we define a linear differential game for a set of interacting agents and solve it to optimality using mixed-integer programming. A disjunctive formulation of the orientation allows us to formulate linear constraints to prevent agent-to-agent collision while preserving the non-holonomic motion properties of the vehicle model. Soft constraints account for prediction errors. We then define a joint cost function, where a cooperation factor can adapt between altruistic, cooperative, and egoistic behavior. We study the influence of the cooperation factor to solve scenarios, where interaction between the agents is necessary to solve them successfully. The approach is then evaluated in a racing scenario, where we show the applicability of the formulation in a closed-loop receding horizon replanning fashion. By accounting for inaccuracies in the cooperative assumption and the actual behavior, we can indeed successfully plan an optimal control strategy interacting closely with other agents.

Optimal Behavior Planning for Autonomous Driving: A Generic Mixed-Integer Formulation

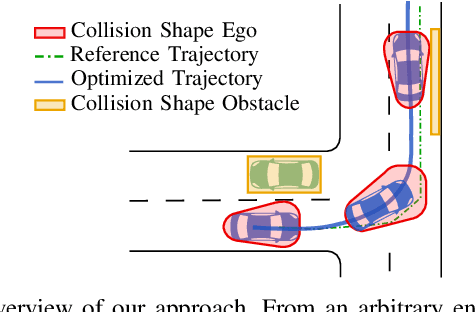
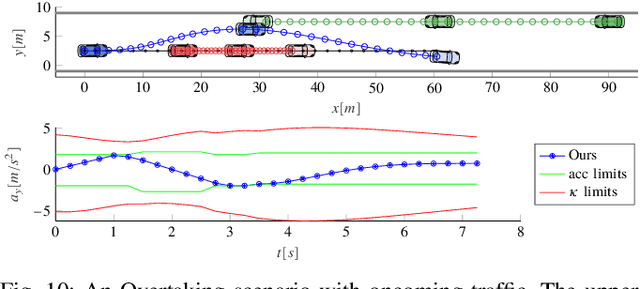
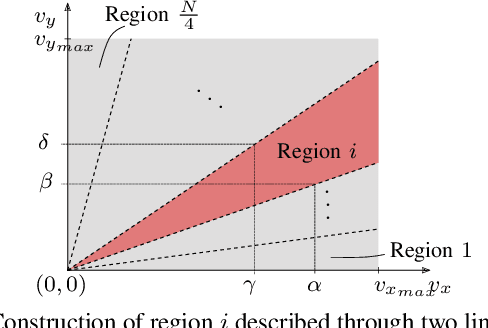
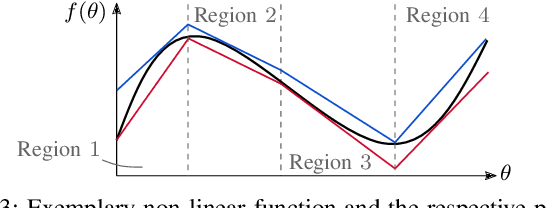
Mixed-Integer Quadratic Programming (MIQP) has been identified as a suitable approach for finding an optimal solution to the behavior planning problem with low runtimes. Logical constraints and continuous equations are optimized alongside. However, it has only been formulated for a straight road, omitting common situations such as taking turns at intersections. This has prevented the model from being used in reality so far. Based on a triple integrator model formulation, we compute the orientation of the vehicle and model it in a disjunctive manner. That allows us to formulate linear constraints to account for the non-holonomy and collision avoidance. These constraints are approximations, for which we introduce the theory. We show the applicability in two benchmark scenarios and prove the feasibility by solving the same models using nonlinear optimization. This new model will allow researchers to leverage the benefits of MIQP, such as logical constraints, or global optimality.

Bridging the Gap between Open Source Software and Vehicle Hardware for Autonomous Driving

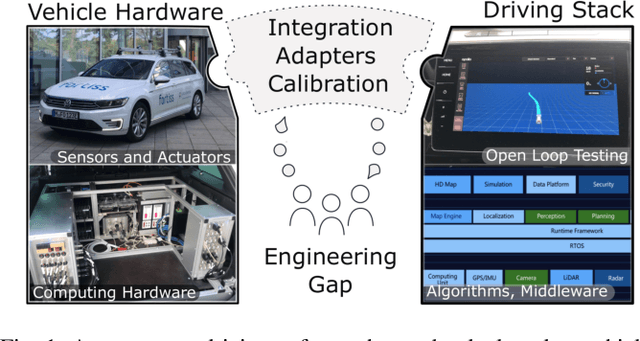
Although many research vehicle platforms for autonomous driving have been built in the past, hardware design, source code and lessons learned have not been made available for the next generation of demonstrators. This raises the efforts for the research community to contribute results based on real-world evaluations as engineering knowledge of building and maintaining a research vehicle is lost. In this paper, we deliver an analysis of our approach to transferring an open source driving stack to a research vehicle. We put the hardware and software setup in context to other demonstrators and explain the criteria that led to our chosen hardware and software design. Specifically, we discuss the mapping of the Apollo driving stack to the system layout of our research vehicle, fortuna, including communication with the actuators by a controller running on a real-time hardware platform and the integration of the sensor setup. With our collection of the lessons learned, we encourage a faster setup of such systems by other research groups in the future.