Optimal Behavior Planning for Autonomous Driving: A Generic Mixed-Integer Formulation
Paper and Code
Mar 30, 2020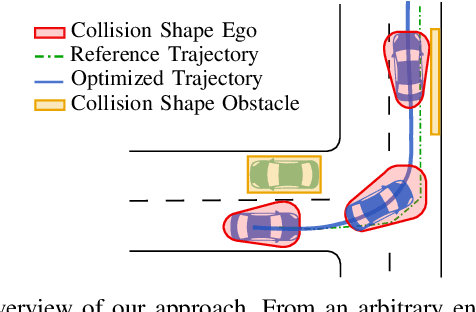
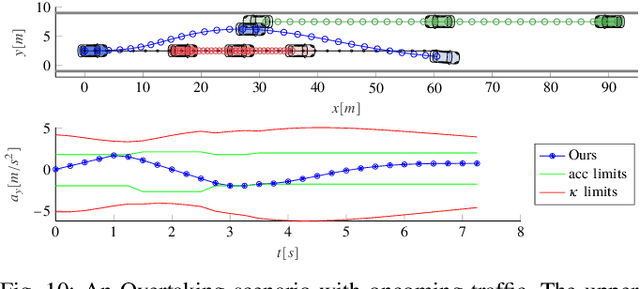
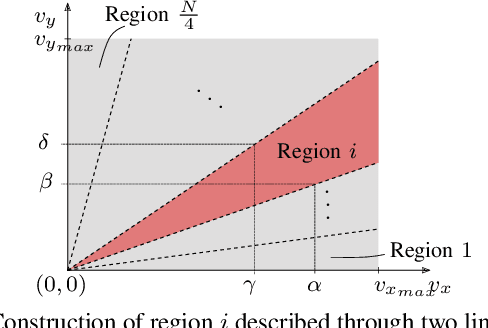
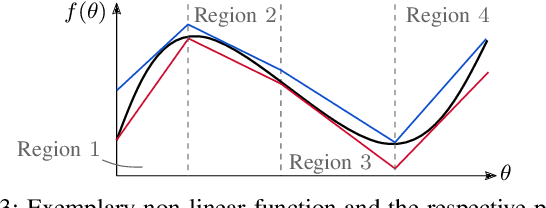
Mixed-Integer Quadratic Programming (MIQP) has been identified as a suitable approach for finding an optimal solution to the behavior planning problem with low runtimes. Logical constraints and continuous equations are optimized alongside. However, it has only been formulated for a straight road, omitting common situations such as taking turns at intersections. This has prevented the model from being used in reality so far. Based on a triple integrator model formulation, we compute the orientation of the vehicle and model it in a disjunctive manner. That allows us to formulate linear constraints to account for the non-holonomy and collision avoidance. These constraints are approximations, for which we introduce the theory. We show the applicability in two benchmark scenarios and prove the feasibility by solving the same models using nonlinear optimization. This new model will allow researchers to leverage the benefits of MIQP, such as logical constraints, or global optimality.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge