A Study in Dataset Distillation for Image Super-Resolution

Dataset distillation is the concept of condensing large datasets into smaller but highly representative synthetic samples. While previous research has primarily focused on image classification, its application to image Super-Resolution (SR) remains underexplored. This exploratory work studies multiple dataset distillation techniques applied to SR, including pixel- and latent-space approaches under different aspects. Our experiments demonstrate that a 91.12% dataset size reduction can be achieved while maintaining comparable SR performance to the full dataset. We further analyze initialization strategies and distillation methods to optimize memory efficiency and computational costs. Our findings provide new insights into dataset distillation for SR and set the stage for future advancements.

Sparsifying Parity-Check Matrices

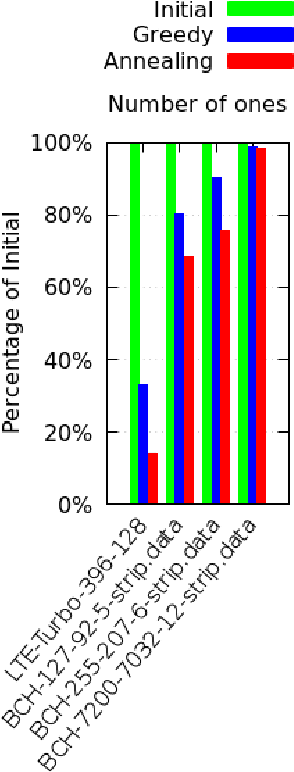
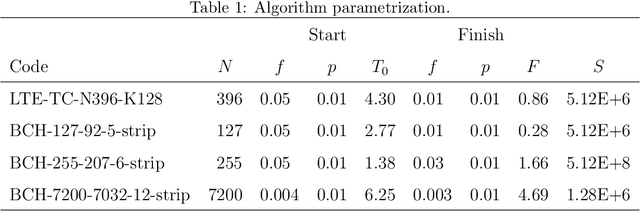
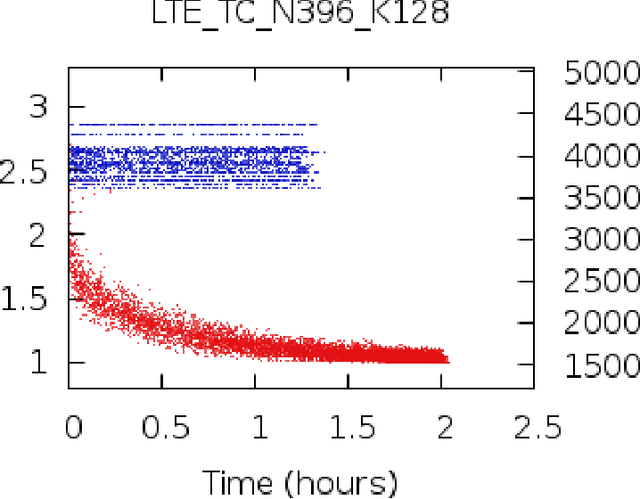
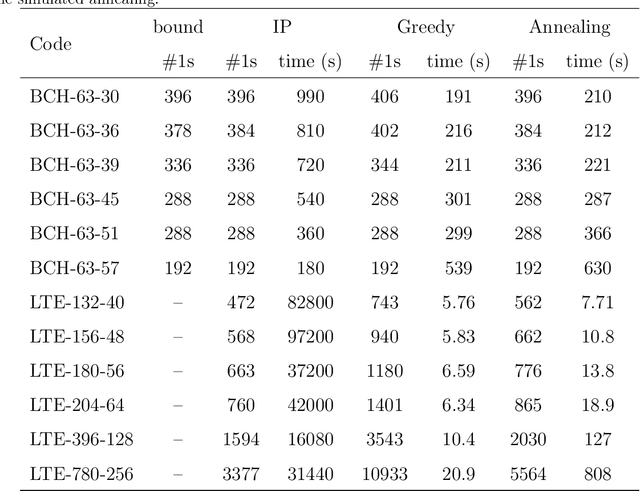
Parity check matrices (PCMs) are used to define linear error correcting codes and ensure reliable information transmission over noisy channels. The set of codewords of such a code is the null space of this binary matrix. We consider the problem of minimizing the number of one-entries in parity-check matrices. In the maximum-likelihood (ML) decoding method, the number of ones in PCMs is directly related to the time required to decode messages. We propose a simple matrix row manipulation heuristic which alters the PCM, but not the code itself. We apply simulated annealing and greedy local searches to obtain PCMs with a small number of one entries quickly, i.e. in a couple of minutes or hours when using mainstream hardware. The resulting matrices provide faster ML decoding procedures, especially for large codes.

The {0,1}-knapsack problem with qualitative levels

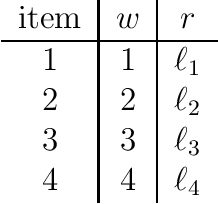
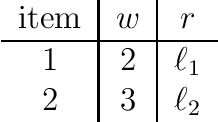
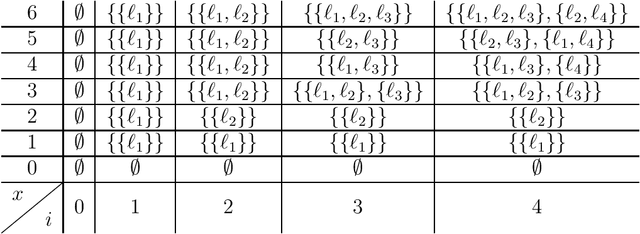
A variant of the classical knapsack problem is considered in which each item is associated with an integer weight and a qualitative level. We define a dominance relation over the feasible subsets of the given item set and show that this relation defines a preorder. We propose a dynamic programming algorithm to compute the entire set of non-dominated rank cardinality vectors and we state two greedy algorithms, which efficiently compute a single efficient solution.