Luís M. S. Russo
Sparsifying Parity-Check Matrices
May 08, 2020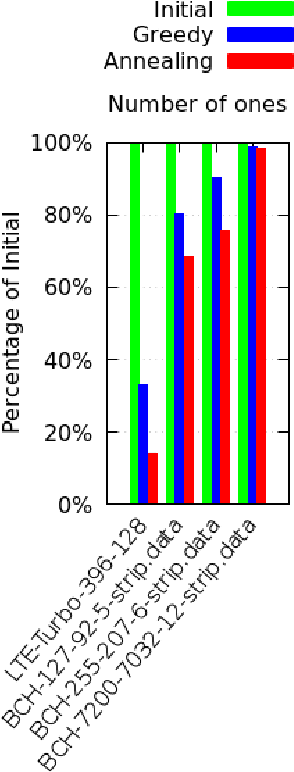
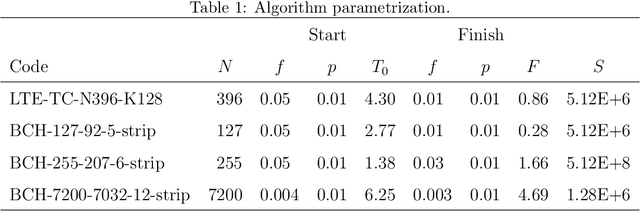
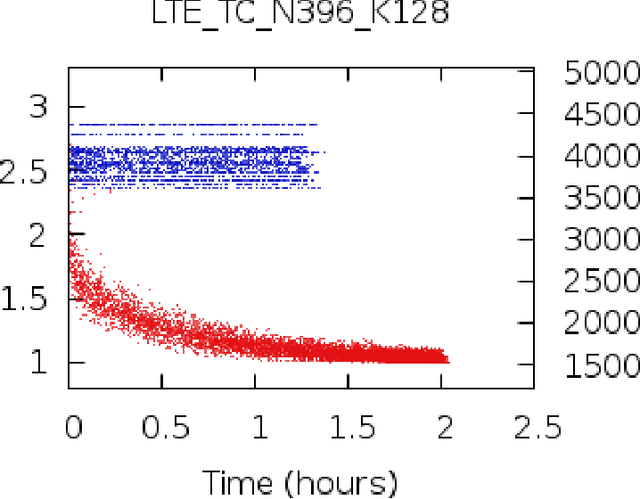
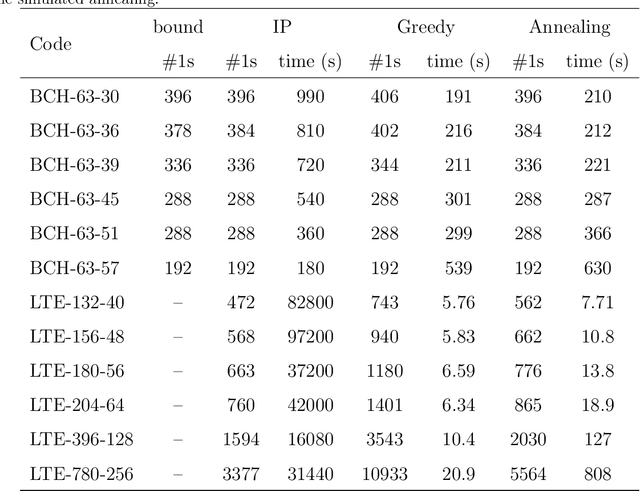
Abstract:Parity check matrices (PCMs) are used to define linear error correcting codes and ensure reliable information transmission over noisy channels. The set of codewords of such a code is the null space of this binary matrix. We consider the problem of minimizing the number of one-entries in parity-check matrices. In the maximum-likelihood (ML) decoding method, the number of ones in PCMs is directly related to the time required to decode messages. We propose a simple matrix row manipulation heuristic which alters the PCM, but not the code itself. We apply simulated annealing and greedy local searches to obtain PCMs with a small number of one entries quickly, i.e. in a couple of minutes or hours when using mainstream hardware. The resulting matrices provide faster ML decoding procedures, especially for large codes.
Quick HyperVolume
Nov 29, 2012



Abstract:We present a new algorithm to calculate exact hypervolumes. Given a set of $d$-dimensional points, it computes the hypervolume of the dominated space. Determining this value is an important subroutine of Multiobjective Evolutionary Algorithms (MOEAs). We analyze the "Quick Hypervolume" (QHV) algorithm theoretically and experimentally. The theoretical results are a significant contribution to the current state of the art. Moreover the experimental performance is also very competitive, compared with existing exact hypervolume algorithms. A full description of the algorithm is currently submitted to IEEE Transactions on Evolutionary Computation.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge