Exact and approximate determination of the Pareto set using minimal correction subsets

Recently, it has been shown that the enumeration of Minimal Correction Subsets (MCS) of Boolean formulas allows solving Multi-Objective Boolean Optimization (MOBO) formulations. However, a major drawback of this approach is that most MCSs do not correspond to Pareto-optimal solutions. In fact, one can only know that a given MCS corresponds to a Pareto-optimal solution when all MCSs are enumerated. Moreover, if it is not possible to enumerate all MCSs, then there is no guarantee of the quality of the approximation of the Pareto frontier. This paper extends the state of the art for solving MOBO using MCSs. First, we show that it is possible to use MCS enumeration to solve MOBO problems such that each MCS necessarily corresponds to a Pareto-optimal solution. Additionally, we also propose two new algorithms that can find a (1 + {\varepsilon})-approximation of the Pareto frontier using MCS enumeration. Experimental results in several benchmark sets show that the newly proposed algorithms allow finding better approximations of the Pareto frontier than state-of-the-art algorithms, and with guaranteed approximation ratios.

Sparsifying Parity-Check Matrices

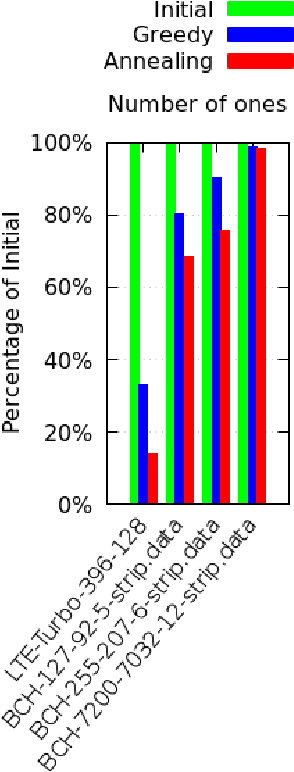
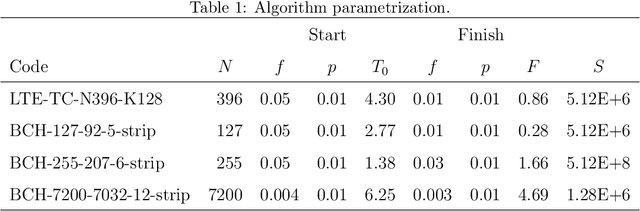
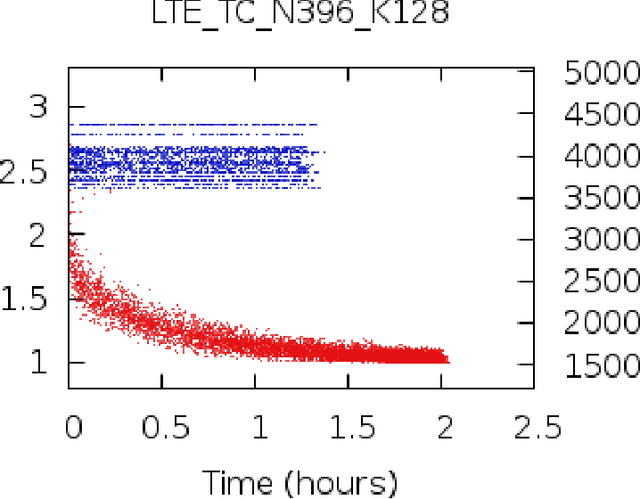
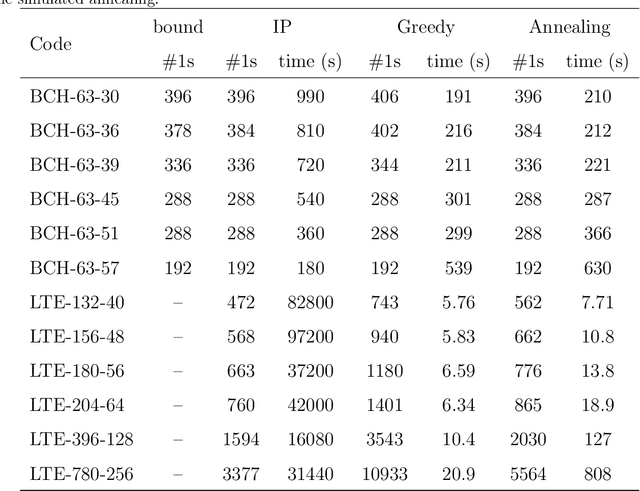
Parity check matrices (PCMs) are used to define linear error correcting codes and ensure reliable information transmission over noisy channels. The set of codewords of such a code is the null space of this binary matrix. We consider the problem of minimizing the number of one-entries in parity-check matrices. In the maximum-likelihood (ML) decoding method, the number of ones in PCMs is directly related to the time required to decode messages. We propose a simple matrix row manipulation heuristic which alters the PCM, but not the code itself. We apply simulated annealing and greedy local searches to obtain PCMs with a small number of one entries quickly, i.e. in a couple of minutes or hours when using mainstream hardware. The resulting matrices provide faster ML decoding procedures, especially for large codes.

The {0,1}-knapsack problem with qualitative levels

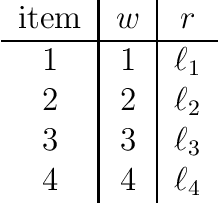
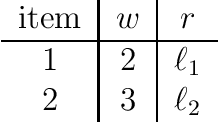
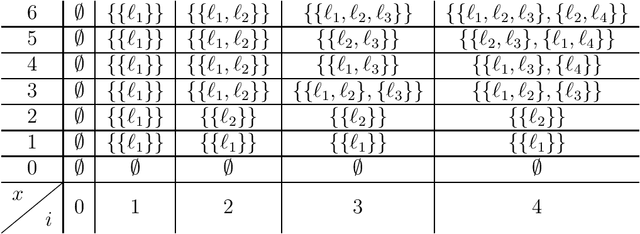
A variant of the classical knapsack problem is considered in which each item is associated with an integer weight and a qualitative level. We define a dominance relation over the feasible subsets of the given item set and show that this relation defines a preorder. We propose a dynamic programming algorithm to compute the entire set of non-dominated rank cardinality vectors and we state two greedy algorithms, which efficiently compute a single efficient solution.

A robust hierarchical nominal classification method based on similarity and dissimilarity

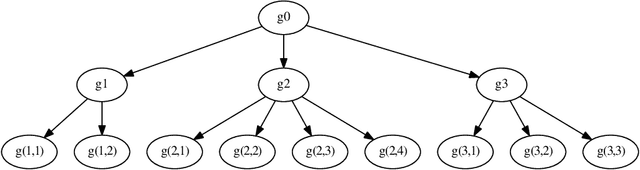
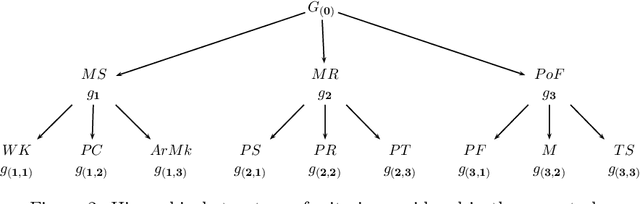
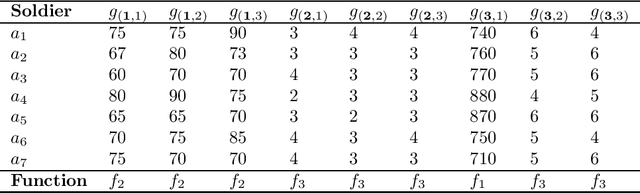
Categorization by Similarity-Dissimilarity is a multiple criteria decision aiding method for dealing with nominal classification problems (predefined and non-ordered categories). Actions are assessed according to multiple criteria and assigned to one or more categories. A set of reference actions is used for defining each category. The assignment of an action to a given category depends on the comparison of the action to the reference set according to a likeness threshold. Distinct sets of criteria weights, interaction coefficients, and likeness thresholds can be defined per category. When applying Cat-SD to complex decision problems, considering a hierarchy of criteria may help to decompose them. We propose to apply Multiple Criteria Hierarchy Process (MCHP) to Cat-SD. An adapted MCHP is proposed to take into account possible interaction effects between criteria structured in a hierarchical way. We also consider an imprecise elicitation of parameters. With the purpose of exploring the assignments obtained by Cat-SD considering possible sets of parameters, we propose to apply the Stochastic Multicriteria Acceptability Analysis (SMAA). The SMAA methodology allows to draw statistical conclusions on the classification of the actions. The proposed method, SMAA-hCat-SD, helps the decision maker to check the effects of the variation of parameters on the classification at different levels of the hierarchy. We propose also a procedure to obtain a final classification fulfilling some requirements by taking into account the hierarchy of criteria and the probabilistic assignments obtained applying SMAA. The application of the proposed method is showed through an example.