A machine learning based algorithm selection method to solve the minimum cost flow problem

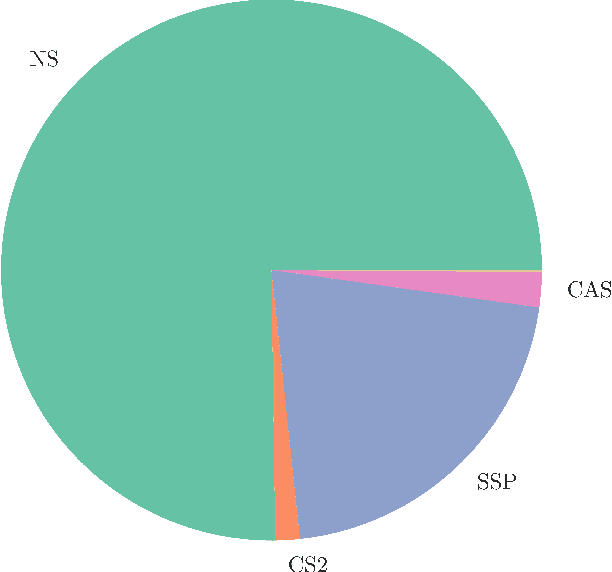
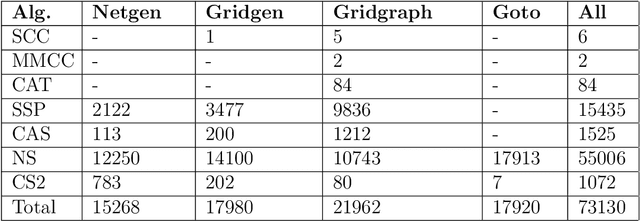
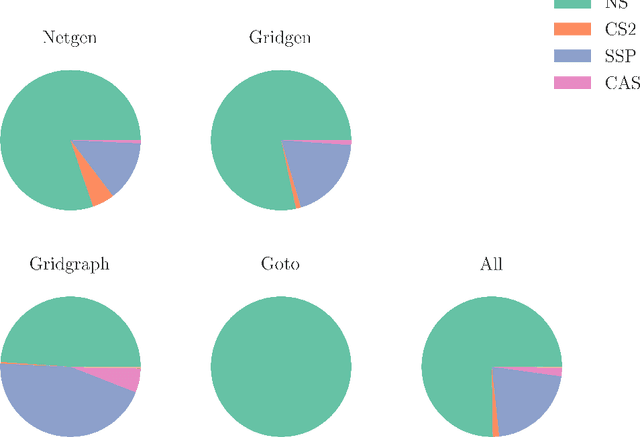
The minimum cost flow problem is one of the most studied network optimization problems and appears in numerous applications. Some efficient algorithms exist for this problem, which are freely available in the form of libraries or software packages. It is noticeable that none of these solvers is better than the other solution methods on all instances. Thus, the question arises whether the fastest algorithm can be selected for a given instance based on the characteristics of the instance. To this end, we train several machine learning classifiers to predict the fastest among a given set of solvers. We accomplish this by creating a representative data set of 81,000 instances and characterizing each of these instances by a vector of relevant features. To achieve better performance, we conduct a grid search to optimize the hyperparameters of the classifiers. Finally, we evaluate the different classifiers by means of accuracy. It is shown that tree-based models appear to adapt and exploit the relevant structures of the minimum-cost flow problem particularly well on a large number of instances, predicting the fastest solver with an accuracy of more than 90%.

Sparsifying Parity-Check Matrices

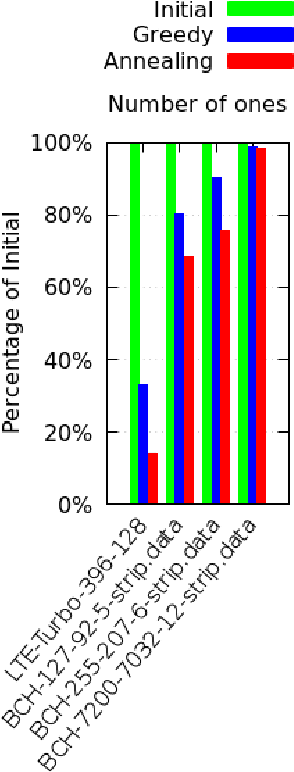
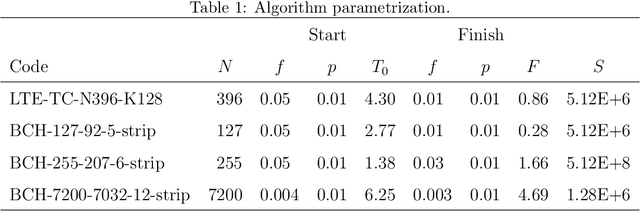
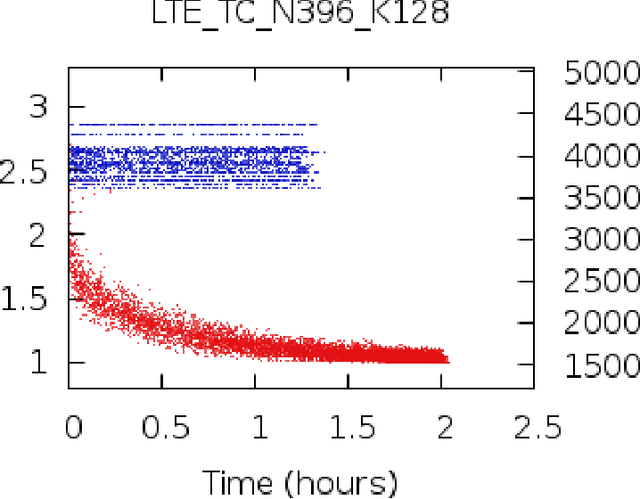
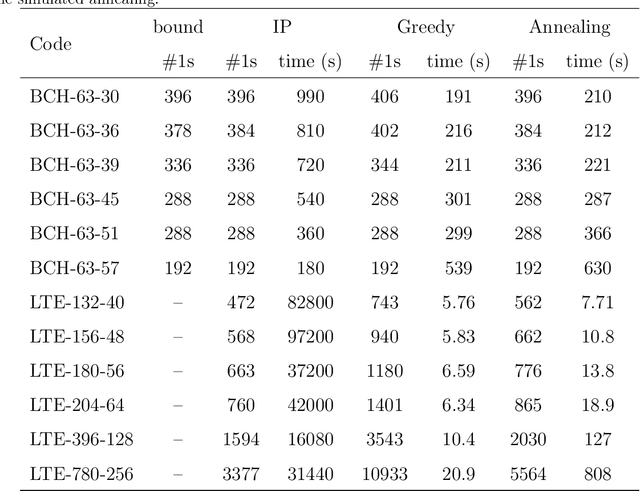
Parity check matrices (PCMs) are used to define linear error correcting codes and ensure reliable information transmission over noisy channels. The set of codewords of such a code is the null space of this binary matrix. We consider the problem of minimizing the number of one-entries in parity-check matrices. In the maximum-likelihood (ML) decoding method, the number of ones in PCMs is directly related to the time required to decode messages. We propose a simple matrix row manipulation heuristic which alters the PCM, but not the code itself. We apply simulated annealing and greedy local searches to obtain PCMs with a small number of one entries quickly, i.e. in a couple of minutes or hours when using mainstream hardware. The resulting matrices provide faster ML decoding procedures, especially for large codes.

The {0,1}-knapsack problem with qualitative levels

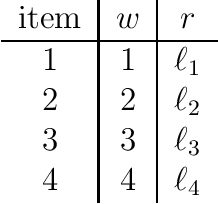
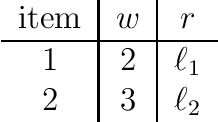
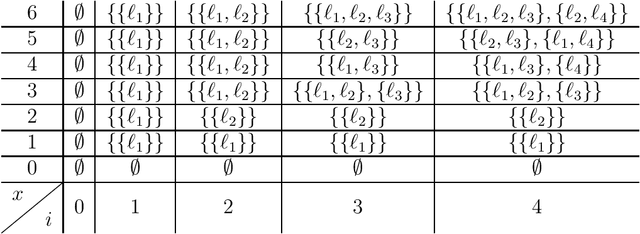
A variant of the classical knapsack problem is considered in which each item is associated with an integer weight and a qualitative level. We define a dominance relation over the feasible subsets of the given item set and show that this relation defines a preorder. We propose a dynamic programming algorithm to compute the entire set of non-dominated rank cardinality vectors and we state two greedy algorithms, which efficiently compute a single efficient solution.